摘要：20． 函数函数f(x)当x=1时有极值. (1) 求m与n的关系表达式, 的单调区间, (3) 当函数y=f(x)的图象上任意一点的切线斜率恒大于3m.求m的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_525632[举报]
(本小题满分14分)
已知函数f (x)=ex，g(x)=lnx，h(x)=kx+b.
(1)当b=0时，若对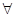
x∈（0，+∞）均有f (x)≥h(x)≥g(x)成立，求实数k的取值范围；
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线，切点分别为(x1, f (x1))和(x2, g(x2))，其中x1>0.
①求证：x1>1>x2；
②若当x≥x1时，关于x的不等式ax2－x+xe
+1≤0恒成立，求实数a的取值范围.
查看习题详情和答案>>
(本小题满分14分)
已知函数f (x)=ex，g(x)=lnx，h(x)=kx+b.
(1)当b=0时，若对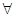
x∈（0，+∞）均有f (x)≥h(x)≥g(x)成立，求实数k的取值范围；
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线，切点分别为(x1, f (x1))和(x2, g(x2))，其中x1>0.
①求证：x1>1>x2；
②若当x≥x1时，关于x的不等式ax2－x+xe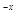
+1≤0恒成立，求实数a的取值范围.
(本小题满分14分)
已知函数f(x)=(1+x)2-aln(1+x)2在(-2,-1)上是增函数，在（-∞，-2）上为减函数.
（1）求f(x)的表达式；
（2）若当x∈
时，不等式f(x)＜m恒成立，求实数m的值；
（3）是否存在实数b使得关于x的方程f(x)=x2+x+b在区间［0，2］上恰好有两个相异的实根，若存在，求实数b的取值范围.
查看习题详情和答案>>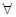
时，不等式f(x)＜m恒成立，求实数m的值；
x∈（0，+∞）均有f (x)≥h(x)≥g(x)成立，求实数k的取值范围；
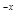+1≤0恒成立，求实数a的取值范围.