摘要:20.在xOy平面上有一点列P1(a1,b1).P2(a2,b2).-.Pn(an,bn).-.对每个正整数n点Pn位于函数y=2000()x(0<a<10)的图象上.且点Pn,点(n,0)与点(n+1,0)构成一个以 Pn为顶点的等腰三角形. (1)求点Pn的纵坐标bn的表达式, (2)若对于每个正整数n,以bn,bn+1,bn+2为边长能构成一个三角形.求a的取值范围, (3)设(n∈N*),若a取(2)中确定的范围内的最小整数.问数列{cn}前多少项的和最大?试说明理由. 答案:(1)由题意知:an=n+,∴bn=2000(). (2)∵函数y=2000()x(0<a<10)递减. ∴对每个自然数n,有bn>bn+1>bn+2.则以 bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn, 即()2+()-1>0, 解得a<-5(1+)或a>5(-1). ∴5(-1)<a<10. (3)∵5(-1)<a<10,∴a=7.∴. ∴数列{cn}是一个递减的等差数列. 由 解得.故数列{cn}前20项和最大.
网址:http://m.1010jiajiao.com/timu3_id_524777[举报]
21.在xoy平面上有一点列P1(a1,b1)、P2(a2,b2),…,Pn(an,bn),…,对每个自然数n,点Pn位于函数y=2000(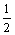 )x(0<a<10)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
)x(0<a<10)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
(1)求点Pn的纵坐标bn的表达式;
(2)若对每个自然数n,以bn,bn-1,bn-2为边长能构成一个三角形,求a的取值范围;
(3)设cn=lg(bn)(n∈N),若a取(2)中确定的范围内的最小整数,问数列{cn}前多少项的和最大?试说明理由.
查看习题详情和答案>>(2000•上海)在XOY平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),…,对每个自然数n,点P,位于函数y=2000(
)n(0<a<10)的图象上,且点Pn,点(n,0)与点(n+1.0)构成一个以Pn为顶点的等腰三角形.
(Ⅰ)求点Pn的纵坐标bn的表达式.
(Ⅱ)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a取值范围.
(Ⅲ)设Bn=b1b2…bn(n∈N).,若a取(2)中确定的范围内的最小整数,求数列{Bn}的最大项的项数.
查看习题详情和答案>>
| a | 10 |
(Ⅰ)求点Pn的纵坐标bn的表达式.
(Ⅱ)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a取值范围.
(Ⅲ)设Bn=b1b2…bn(n∈N).,若a取(2)中确定的范围内的最小整数,求数列{Bn}的最大项的项数.
在XOY平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),…,对每个自然数n,点P,位于函数 的图象上,且点Pn,点(n,0)与点(n+1.0)构成一个以Pn为顶点的等腰三角形.
的图象上,且点Pn,点(n,0)与点(n+1.0)构成一个以Pn为顶点的等腰三角形.
(Ⅰ)求点Pn的纵坐标bn的表达式.
(Ⅱ)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a取值范围.
(Ⅲ)设Bn=b1b2…bn(n∈N).,若a取(2)中确定的范围内的最小整数,求数列{Bn}的最大项的项数.
查看习题详情和答案>>
 的图象上,且点Pn,点(n,0)与点(n+1.0)构成一个以Pn为顶点的等腰三角形.
的图象上,且点Pn,点(n,0)与点(n+1.0)构成一个以Pn为顶点的等腰三角形.(Ⅰ)求点Pn的纵坐标bn的表达式.
(Ⅱ)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a取值范围.
(Ⅲ)设Bn=b1b2…bn(n∈N).,若a取(2)中确定的范围内的最小整数,求数列{Bn}的最大项的项数.
查看习题详情和答案>>
(2000•上海)在xoy平面上有一点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn),…,对每个自然数n,点Pn位于函数y=2000(
)x,(0<a<10)的图象上,且点Pn、点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
(Ⅰ)求点Pn的纵坐标bn的表达式;
(Ⅱ)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(Ⅲ)设Cn=lg(bn),n∈N*,若a取(Ⅱ)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由.(lg2=0.3010,lg7=0.8450)
查看习题详情和答案>>
| a | 10 |
(Ⅰ)求点Pn的纵坐标bn的表达式;
(Ⅱ)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(Ⅲ)设Cn=lg(bn),n∈N*,若a取(Ⅱ)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由.(lg2=0.3010,lg7=0.8450)