摘要: 在平面直角坐标系中.直线y = –2x + 5上有一系列点:P0 , P1 (x1, y1), P2 (x2, y2), --.P n (x n , y n), --.已知数列{}是首项为.公差为1的等差数列. (1)求数列{x n} (n∈N*)及数列{y n} (n∈N*)的通项公式, (2)是否存在一个半径最小的圆C.使得对一切n∈N*.点P n (x n , y n)均在此圆的内部?若存在.求出此圆的方程,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_523306[举报]
(本小题满分15分)平面直角坐标系xOy中,已知⊙M经过点F1(0,-c),F2(0,c),A( c,0)三点,其中c>0.
c,0)三点,其中c>0.
(1)求⊙M的标准方程(用含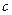 的式子表示);
的式子表示);
(2)已知椭圆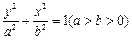 (其中
(其中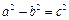 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,
⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
 c,0)三点,其中c>0.
c,0)三点,其中c>0.(1)求⊙M的标准方程(用含
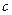 的式子表示);
的式子表示);(2)已知椭圆
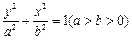 (其中
(其中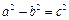 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
(本题满分15分)
在平面直角坐标系xOy中,已知对于任意实数 ,直线
,直线 恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为
恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为 .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O: 与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
查看习题详情和答案>>
(本题满分15分)
在平面直角坐标系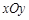 中,点
中,点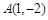 ,
,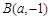 ,
,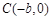 ,且
,且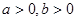 .
.
(1)若点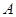 、
、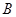 、
、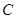 在直线
在直线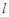 上,求
上,求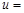
 的最小值,并求此时直线
的最小值,并求此时直线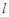 的方程;
的方程;
(2)若以线段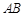 、
、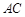 为邻边的平行四边形两条对角线的长相等,且
为邻边的平行四边形两条对角线的长相等,且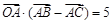 ,求
,求 、
、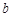 的值.
的值.
查看习题详情和答案>>