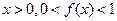摘要:设函数f(x)定义在R上.对任意m.n恒有f(m+n)=f(m)·f(n).且当x>0时.0<f(x)<1. (1)求证:f(0)=1.且当x<0时.f(x)>1, (2)求证:f(x)在R上单调递减, (3)设集合A={ (x.y)|f(x2)·f(y2)>f(1)}.集合B={(x.y)|f(ax-g+2)=1.a∈R}.若A∩B=.求a的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_521773[举报]
设函数f(x)定义在R上,对任意m、n恒有f(m+n)=f(m)·f(n),且当x>0时,0<f(x)<1.
(1)求证: f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上单调递减;
(3)设集合A={ (x,y)|f(x2)·f(y2)>f(1)},集合B={(x,y)|f(ax-g+2)=1,a∈R},若A∩B=![]() ,求a的取值范围.
,求a的取值范围.
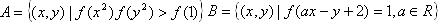
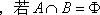 ,确定a的取值范围.
,确定a的取值范围. 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有 且当
且当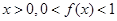
 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有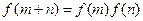 且当
且当