摘要：22．已知抛物线的焦点为.过作两条互相垂直的弦..设.的中点分别为 (1) 求证:直线必过定点.并求出定点坐标 (2) 分别以和为直径作圆.求两圆相交弦中点的轨迹方程 解:(1)证明:由题可知.设..直线AB的方程为.则由消去x可得 . 所以..即.代入方程.解得.所以.点M的坐标为 同理可得:的坐标为 直线的方程为.整理得 显然.不论为何值.均满足方程.所以直线恒过定点 (2)过作准线的垂线.垂足分别为 由抛物线的性质不难知道:准线为圆与圆的公切线.设两圆的相交弦交公切线于点.则由平面几何的知识可知:为的中点 所以 . 即 又因为公共弦必与两圆的连心线垂直.所以公共弦的斜率为 所以.公共弦所在直线的方程为 即 所以公共弦恒过原点 根据平面几何的知识知道:公共弦中点就是公共弦与两圆连心线的交点.所以原点.定点.所求点构成以为直角顶点的直角三角形.即在以为直径的圆上 又对于圆上任意一点.必可利用方程求得值.从而以上步步可逆.故所求轨迹方程为
网址：http://m.1010jiajiao.com/timu3_id_521199[举报]
(本小题满分14分)
已知F1，F2分别是椭圆＋＝1的左、右焦点，曲线C是以坐标原点为顶点，以F2为焦点的抛物线，自点F1引直线交曲线C于P、Q两个不同的交点，点P关于x轴的对称点记为M.设＝λ.
(Ⅰ)求曲线C的方程；
(Ⅱ)证明：＝－λ；
(Ⅲ)若λ∈[2,3]，求|PQ|的取值范围.
查看习题详情和答案>>
(本小题满分14分)
设
椭圆方程为
抛物线方程为
如图4所示，过点
作
轴的平行线，与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
（1）求满足条件的椭圆方程和抛物线方程；
（2）设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得
为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标) 。
(本小题满分14分)设b>0，椭圆方程为
，抛物线方程为
.如图4所示,过点F(0,b+2)作x轴的平行线，与抛物线在
第一象限的交点为G.已知抛物线在点G的切线经
过椭圆的右焦点
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点，试探究在
抛物线上是否存在点P，使得△ABP为直角三角形？
若存在，请指出共有几个这样的点？并说明理由
（不必具体求出这些点的坐标）.
查看习题详情和答案>>
椭圆方程为
抛物线方程为
如图4所示，过点
作
轴的平行线，与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标) 。
椭圆方程为
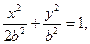抛物线方程为
如图4所示，过点
作
轴的平行线，与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标) 。