网址:http://m.1010jiajiao.com/timu3_id_519681[举报]
(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
查看习题详情和答案>>(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
查看习题详情和答案>>零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
查看习题详情和答案>>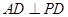 ,BC=1,
,BC=1, ,PD=CD=2.
,PD=CD=2.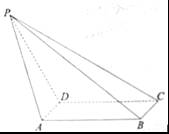
 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。