题目内容
零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
【解析】本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查空间想象能力,运算能力和推理论证能力.满分12分.
(I)解:因为四边形ADEF是正方形,所以FA//ED.故![]() 为异面直线CE与AF所成的角.
为异面直线CE与AF所成的角.
因为FA![]() 平面ABCD,所以FA
平面ABCD,所以FA![]() CD.故ED
CD.故ED![]() CD.
CD.
在Rt△CDE中,CD=1,ED=![]() ,CE=
,CE=![]() =3,故cos
=3,故cos![]() =
=![]() =
=![]() .
.
所以异面直线CE和AF所成角的余弦值为![]() .
.
(Ⅱ)证明:过点B作BG//CD,交AD于点G,则![]() .由
.由![]() ,可得BG
,可得BG![]() AB,从而CD
AB,从而CD![]() AB,又CD
AB,又CD![]() FA,FA
FA,FA![]() AB=A,所以CD
AB=A,所以CD![]() 平面ABF.
平面ABF.
(Ⅲ)解:由(Ⅱ)及已知,可得AG=![]() ,即G为AD的中点.取EF的中点N,连接GN,则GN
,即G为AD的中点.取EF的中点N,连接GN,则GN![]() EF,因为BC//AD,所以BC//EF.过点N作NM
EF,因为BC//AD,所以BC//EF.过点N作NM![]() EF,交BC于M,则
EF,交BC于M,则![]() 为二面角B-EF-A的平面角。
为二面角B-EF-A的平面角。
连接GM,可得AD![]() 平面GNM,故AD
平面GNM,故AD![]() GM.从而BC
GM.从而BC![]() GM.由已知,可得GM=
GM.由已知,可得GM=![]() .由NG//FA,FA
.由NG//FA,FA![]() GM,得NG
GM,得NG![]() GM.
GM.
在Rt△NGM中,tan![]() ,
,
所以二面角B-EF-A的正切值为![]() .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.51 | 1.47 | 1.46 | 1.53 | 1.47 |
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;
(ⅱ)求这2个零件直径相等的概率.

 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;  满分12分)
满分12分)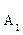 ,
,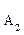 ,…
,…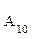 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据: