题目内容
已知椭圆 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。
(I)求椭圆的离心率。
(II)设A为椭圆的右顶点,O为坐标原点,若Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值。
【考点定位】本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面内两点间距离公式等基础知识. 考查用代数方法研究圆锥曲线的性质,以及数形结合的数学思想方法.考查运算求解能力、综合分析和解决问题的能力.
【答案】
(1)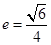 (2)
(2)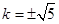
【解析】
(I)
解:因为点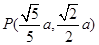 在椭圆上,故
在椭圆上,故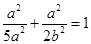 .可得
.可得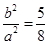
于是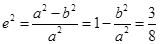 ,所以椭圆的离心率
,所以椭圆的离心率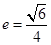
(II)解:设直线OQ的斜率为k,则其方程为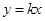 .设点Q的坐标为
.设点Q的坐标为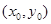
由条件得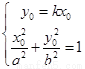 消去
消去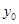 并整理得
并整理得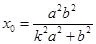 ①
①
由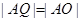 ,
,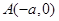 及
及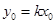 ,
,
得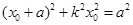 .
.
整理得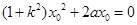 .而
.而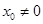 ,于是
,于是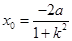 ,代入①,
,代入①,
整理得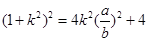
由(I)知,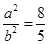 故
故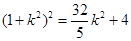 ,即
,即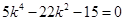 ,可得
,可得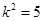 .
.
所以直线OQ的斜率为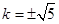

练习册系列答案
相关题目
 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上. (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
 ,求直线l的倾斜角;
,求直线l的倾斜角; 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且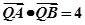 .求
.求 的值.
的值.