摘要:19. 解:(1)延长B1E交BC于F, ∵ΔB1EC∽ΔFEB, BE=EC1 ∴BF=B1C1=BC.从而F为BC的中点. ∵G为ΔABC的重心.∴A.G.F三点共线.且= =.∴GE∥AB1. 又GE侧面AA1B1B. ∴GE∥侧面AA1B1B (2)在侧面AA1B1B内.过B1作B1H⊥AB.垂足为H.∵侧面AA1B1B⊥底面ABC. ∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角. AA1= 2. ∴∠B1BH=600.BH=1.B1H=. 在底面ABC内.过H作HT⊥AF.垂足为T.连B1T.由三垂线定理有B1T⊥AF. 又平面B1GE与底面ABC的交线为AF.∴∠B1TH为所求二面角的平面角. ∴AH=AB+BH=3.∠HAT=300. ∴HT=AHsin300=. 在RtΔB1HT中.tan∠B1TH== . 从而平面B1GE与底面ABC所成锐二面角的大小为arctan
网址:http://m.1010jiajiao.com/timu3_id_518818[举报]
 (1)(如图1)在边长为4的正方形ABCD中,E、F分别是边AB,BC上的点,且AE=BF=1,过线段EF上的点P分别作DC,AD的垂线,垂足为M,N,延长NP交BC于Q,试写出矩形PMDN的面积y与FQ的长x之间的函数关系,并求出y的最大值.
(1)(如图1)在边长为4的正方形ABCD中,E、F分别是边AB,BC上的点,且AE=BF=1,过线段EF上的点P分别作DC,AD的垂线,垂足为M,N,延长NP交BC于Q,试写出矩形PMDN的面积y与FQ的长x之间的函数关系,并求出y的最大值.(2)(如图2)在边长为4的正方形ABCD中,E、F分别是边AB,BC上的点,且AE=BF=x,设多边形的面积为y,当x为何值时,多边形AEFCD的面积最小?
 于
于 (不同于点
(不同于点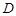 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥 ,如图2所示.
,如图2所示.
 //平面
//平面 ;
; ;
; 平面
平面 ,试判断直线
,试判断直线 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由.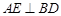 于
于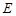 (不同于点
(不同于点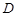 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥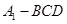 ,如图2所示.
,如图2所示.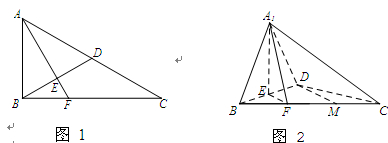
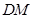 //平面
//平面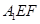 ;
;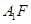 ;
;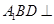 平面
平面 ,试判断直线
,试判断直线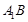 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由.