题目内容
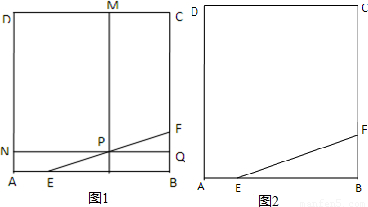
（1）（如图1）在边长为4的正方形ABCD中，E、F分别是边AB，BC上的点，且AE=BF=1，过线段EF上的点P分别作DC，AD的垂线，垂足为M，N，延长NP交BC于Q，试写出矩形PMDN的面积y与FQ的长x之间的函数关系，并求出y的最大值．（2）（如图2）在边长为4的正方形ABCD中，E、F分别是边AB，BC上的点，且AE=BF=x，设多边形的面积为y，当x为何值时，多边形AEFCD的面积最小？
分析：（1）根据图象中的平行关系，确定矩形的边长，进而可求面积，由此可得面积的最值；
（2）确定多边形AEFCD的面积，利用基本不等式可求最值．
（2）确定多边形AEFCD的面积，利用基本不等式可求最值．
解答：解：（1）由题意，∵PQ∥BE，∴
=
，∴PQ=3x，∴PN=4-3x
∵DN=4-AN=4-（1-x）=3+x，
∴矩形PMDN的面积y=（4-3x）（3+x）（0≤x≤1）
∴y=-3(x+
)2+
∵0≤x≤1，∴x=0时，ymax=12；
（2）多边形AEFCD的面积等于正方形的面积减去三角形的面积，所以y=16-
（4-x）x
∵
（4-x）x≤
(
)2=2（当且仅当x=2时，取等号）
∴y≥16-2=14
∴x=2时，ymin=14
| x |
| 1 |
| PQ |
| 3 |
∵DN=4-AN=4-（1-x）=3+x，
∴矩形PMDN的面积y=（4-3x）（3+x）（0≤x≤1）
∴y=-3(x+
| 5 |
| 6 |
| 169 |
| 12 |
∵0≤x≤1，∴x=0时，ymax=12；
（2）多边形AEFCD的面积等于正方形的面积减去三角形的面积，所以y=16-
| 1 |
| 2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
| 4-x+x |
| 2 |
∴y≥16-2=14
∴x=2时，ymin=14
点评：本题考查面积的计算，考查函数模型的构建，考查函数最值的求解，属于中档题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
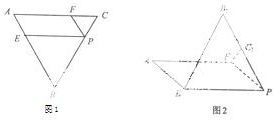如图1，在边长为3的正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE=CF=CP=1，今将△BEP、△CFP分别沿EP、FP向上折起，使边BP与边CP所在的直线重合（如图2），B、C折后的对应点分别记为B、C1．
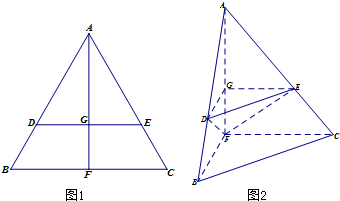（2013•广东）如图1，在边长为1的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A-BCF，其中
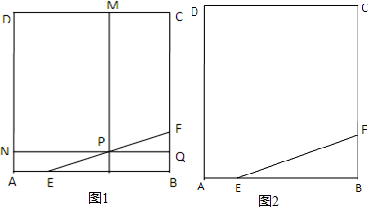（1）（如图1）在边长为4的正方形ABCD中，E、F分别是边AB，BC上的点，且AE=BF=1，过线段EF上的点P分别作DC，AD的垂线，垂足为M，N，延长NP交BC于Q，试写出矩形PMDN的面积y与FQ的长x之间的函数关系，并求出y的最大值．