摘要:解:(1)定义域为关于原点对称.为奇函数, (2)当时. 原不等式解集: 当时. 原不等式解集:
网址:http://m.1010jiajiao.com/timu3_id_518817[举报]
已知函数 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①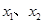 、
、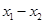 是定义域中的数时,有
是定义域中的数时,有 ;
;
②
 是定义域中的一个数);
是定义域中的一个数);
③当 时,
时, .
.
(1)判断 与
与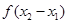 之间的关系,并推断函数
之间的关系,并推断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)当函数 的定义域为
的定义域为 时,
时,
①求 的值;②求不等式
的值;②求不等式 的解集.
的解集.
查看习题详情和答案>>
已知函数 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①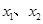 、
、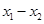 是定义域中的数时,有
是定义域中的数时,有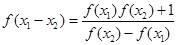 ;
;
②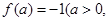
 是定义域中的一个数);
是定义域中的一个数);
③当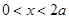 时,
时,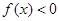 .
.
(1)判断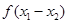 与
与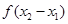 之间的关系,并推断函数
之间的关系,并推断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在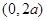 上的单调性,并证明;
上的单调性,并证明;
(3)当函数 的定义域为
的定义域为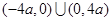 时,
时,
①求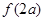 的值;②求不等式
的值;②求不等式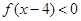 的解集.
的解集.
已知函数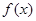 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①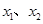 、
、 是定义域中的数时,有
是定义域中的数时,有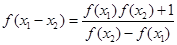 ;
;
②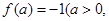
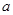 是定义域中的一个数);
是定义域中的一个数);
③当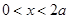 时,
时,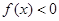 .
.
(1)判断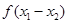 与
与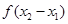 之间的关系,并推断函数
之间的关系,并推断函数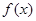 的奇偶性;
的奇偶性;
(2)判断函数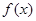 在
在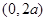 上的单调性,并证明;
上的单调性,并证明;
(3)当函数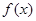 的定义域为
的定义域为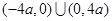 时,
时,
①求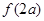 的值;②求不等式
的值;②求不等式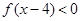 的解集.
的解集.
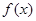 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:①
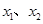 、
、 是定义域中的数时,有
是定义域中的数时,有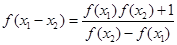 ;
;②
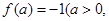
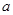 是定义域中的一个数);
是定义域中的一个数);③当
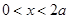 时,
时,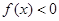 .
.(1)判断
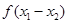 与
与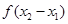 之间的关系,并推断函数
之间的关系,并推断函数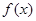 的奇偶性;
的奇偶性;(2)判断函数
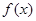 在
在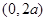 上的单调性,并证明;
上的单调性,并证明;(3)当函数
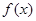 的定义域为
的定义域为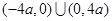 时,
时,①求
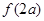 的值;②求不等式
的值;②求不等式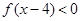 的解集.
的解集.  ;
;