题目内容
已知函数 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①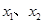 、
、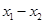 是定义域中的数时,有
是定义域中的数时,有 ;
;
②
 是定义域中的一个数);
是定义域中的一个数);
③当 时,
时, .
.
(1)判断 与
与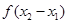 之间的关系,并推断函数
之间的关系,并推断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)当函数 的定义域为
的定义域为 时,
时,
①求 的值;②求不等式
的值;②求不等式 的解集.
的解集.
【答案】
(1)略
(2)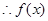 在
在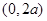 上是增函数;
上是增函数;
(3)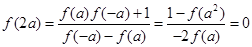 ,不等式的解集是
,不等式的解集是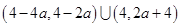 .
.
【解析】(1) 不妨令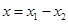 ,则
,则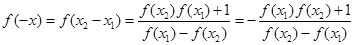
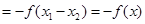 ,
,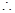
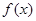 是奇函数;
是奇函数;
(2)在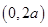 上任取两个实数
上任取两个实数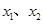 ,且
,且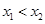 ,则有
,则有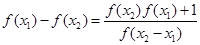 ,然后再根据x1和x2的范围,分别讨论差值符号,进行证明出f(x)单调性.
,然后再根据x1和x2的范围,分别讨论差值符号,进行证明出f(x)单调性.
(3)先根据条件得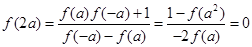 ,所以
,所以
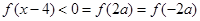 ,然后再利用f(x)的单调性去掉法则符合f转化为关于x的一次不等式即可.
,然后再利用f(x)的单调性去掉法则符合f转化为关于x的一次不等式即可.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为R,且当
的定义域为R,且当 时,
时, 恒成立,
恒成立, 对称;
对称; 图象的一个对称点。
图象的一个对称点。 的定义域为
的定义域为 ,值域为
,值域为 .下列关于函数
.下列关于函数 时,
时, ;②将
;②将 ,得到的图像必定是一条连续的曲线;③
,得到的图像必定是一条连续的曲线;③ 上的单调函数;④
上的单调函数;④




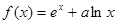 的定义域是D,关于函数
的定义域是D,关于函数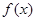 给出下列命题:
给出下列命题: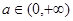 ,函数
,函数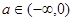 ,函数
,函数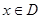 ,都有
,都有