摘要:一元二次方程根的分布理论.方程在上有两根.在上有两根.在和上各有一根的充要条件分别是什么? (..).根的分布理论成立的前提是开区间.若在闭区间讨论方程有实数解的情况.可先利用在开区间上实根分布的情况.得出结果.再令和检查端点的情况.
网址:http://m.1010jiajiao.com/timu3_id_518059[举报]
已知a,b,c∈R,且三次方程f(x)=x3-ax2+bx-c=0有三个实根x1,x2,x3.
(1)类比一元二次方程根与系数的关系,写出此方程根与系数的关系;
(2)若a∈Z,b∈Z且|b|<2,f(x)在x=α,x=β处取得极值且-1<α<0<β<1,试求此方程三个根两两不等时c的取值范围.
查看习题详情和答案>>
(1)类比一元二次方程根与系数的关系,写出此方程根与系数的关系;
(2)若a∈Z,b∈Z且|b|<2,f(x)在x=α,x=β处取得极值且-1<α<0<β<1,试求此方程三个根两两不等时c的取值范围.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2= .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
AB=|x1-x2|= =
= =
= =
= .
.

参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0)、B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
查看习题详情和答案>>
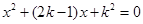 。求使方程有两个大于1的实数根的充要条件。
。求使方程有两个大于1的实数根的充要条件。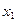 与
与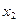 分别是实系数一元二次方程
分别是实系数一元二次方程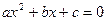 和
和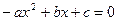 的一个实根,且
的一个实根,且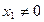 ,
,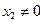 .求证:方程
.求证:方程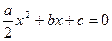 必有一根介于
必有一根介于