题目内容
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2= .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
AB=|x1-x2|= =
= =
= =
= .
.

参考以上定理和结论,解答下列问题:
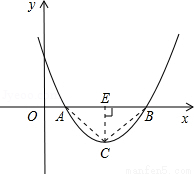
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0)、B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
【答案】
(1) 4;(2) 12
【解析】
解:(1)当△ABC为直角三角形时,过C作CE⊥AB于E,则AB=2CE.
∵抛物线与x轴有两个交点,△=b2-4ac>0,则|b2-4ac|=b2-4ac.
∵a>0,∴AB=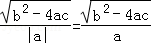 ,
,
又∵CE=|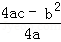 |=
|= ,
,
∴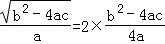 ,
,
∴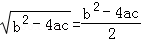 ,
,
∴ ,
,
∵b2-4ac>0,
∴b2-4ac=4;
(2)当△ABC为等边三角形时,
由(1)可知CE= ,
,
∴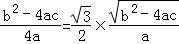 ,
,
∵b2-4ac>0,
∴b2-4ac=12.

练习册系列答案
相关题目
 某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点
某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点