摘要:(三)两条直线的位置关系 1. 判定两条直线的位置关系 设, , (1)或仅有一个不存在 或一个为零一个不存在 (2)且或均不存在且 (3)与重合且或均不存在且 [例题] 已知两直线,.当为何值时.与重合 解:当时.则 ∴ (1)当时., ∴ (2)当时., ∴ (3)当时., ∴ 重合 (4)当..时.相交. 说明:时.与平行或重合相交且只有有数几个值应先分析. 2. 两条直线所成的角与直线到的角 夹角: 到的角: 3. 点到直线的距离: 到的距离为,到的距离为.两条平行线,.则与的距离
网址:http://m.1010jiajiao.com/timu3_id_517911[举报]
设抛物线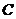 的方程为
的方程为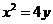 ,
,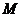 为直线
为直线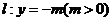 上任意一点,过点
上任意一点,过点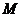 作抛物线
作抛物线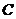 的两条切线
的两条切线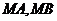 ,切点分别为
,切点分别为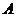 ,
,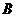 .
.
(1)当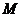 的坐标为
的坐标为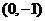 时,求过
时,求过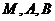 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线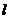 与此圆的位置关系;
与此圆的位置关系;
(2)求证:直线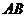 恒过定点;
恒过定点;
(3)当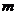 变化时,试探究直线
变化时,试探究直线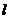 上是否存在点
上是否存在点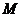 ,使
,使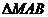 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
查看习题详情和答案>>
(本题满分14分)设抛物线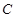 的方程为
的方程为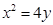 ,
,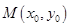 为直线
为直线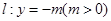 上任意一点,过点
上任意一点,过点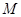 作抛物线
作抛物线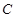 的两条切线
的两条切线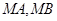 ,切点分别为
,切点分别为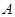 ,
,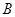 .
.
(1)当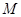 的坐标为
的坐标为 时,求过
时,求过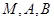 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线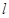 与此圆的位置关系;
与此圆的位置关系;
(2)求证:直线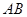 恒过定点
恒过定点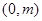 .
.
查看习题详情和答案>>
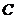 的方程为
的方程为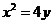 ,
, 为直线
为直线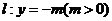 上任意一点,过点
上任意一点,过点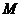 作抛物线
作抛物线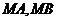 ,切点分别为
,切点分别为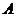 ,
,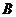 .
.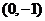 时,求过
时,求过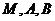 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线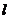 与此圆的位置关系;
与此圆的位置关系; 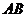 恒过定点
恒过定点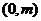 .
.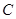 的方程为
的方程为 ,
, 为直线
为直线 上任意一点,过点
上任意一点,过点 ,切点分别为
,切点分别为 ,
, .
. 时,求过
时,求过 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线 与此圆的位置关系;
与此圆的位置关系;
 恒过定点;
恒过定点; 变化时,试探究直线
变化时,试探究直线 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.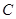 的方程为
的方程为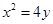 ,
,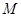 为直线
为直线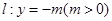 上任意一点,过点
上任意一点,过点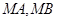 ,切点分别为
,切点分别为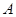 ,
,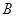 .
.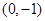 时,求过
时,求过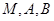 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线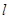 与此圆的位置关系;
与此圆的位置关系; 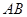 恒过定点;
恒过定点;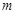 变化时,试探究直线
变化时,试探究直线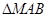 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.