题目内容
设抛物线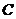 的方程为
的方程为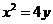 ,
,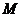 为直线
为直线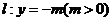 上任意一点,过点
上任意一点,过点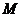 作抛物线
作抛物线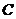 的两条切线
的两条切线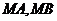 ,切点分别为
,切点分别为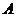 ,
,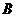 .
.
(1)当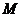 的坐标为
的坐标为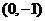 时,求过
时,求过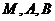 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线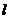 与此圆的位置关系;
与此圆的位置关系;
(2)求证:直线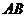 恒过定点;
恒过定点;
(3)当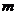 变化时,试探究直线
变化时,试探究直线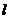 上是否存在点
上是否存在点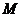 ,使
,使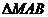 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
(本小题满分14分)
解:(1)当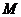 的坐标为
的坐标为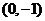 时,设过
时,设过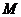 点的切线方程为
点的切线方程为 ,代入
,代入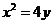 ,整理得
,整理得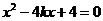 ,
,
令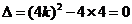 ,解得
,解得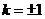 ,
,
代入方程得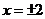 ,故得
,故得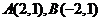 , .................2分
, .................2分
因为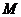 到
到 的中点
的中点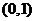 的距离为
的距离为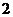 ,
,
从而过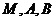 三点的圆的方程为
三点的圆的方程为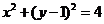 .
.
易知此圆与直线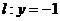 相切.
..................4分
相切.
..................4分
(2)证法一:设切点分别为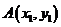 ,
,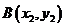 ,过抛物线上点
,过抛物线上点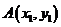 的切线方程为
的切线方程为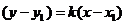 ,代入
,代入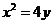 ,整理得
,整理得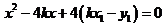
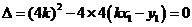 ,又因为
,又因为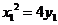 ,所以
,所以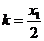 ................5分
................5分
从而过抛物线上点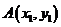 的切线方程为
的切线方程为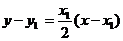 即
即
又切线过点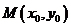 ,所以得
,所以得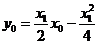 ① 即
① 即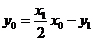
同理可得过点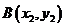 的切线为
的切线为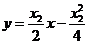 ,
,
又切线过点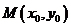 ,所以得
,所以得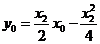 ② 即
② 即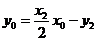 .................6分
.................6分
即点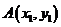 ,
,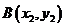 均满足
均满足 即
即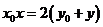 ,故直线
,故直线 的方程为
的方程为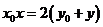 .................7分
.................7分
又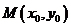 为直线
为直线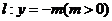 上任意一点,故
上任意一点,故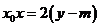 对任意
对任意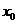 成立,所以
成立,所以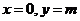 ,从而直线
,从而直线 恒过定点
恒过定点 ..................8分
..................8分
证法二:设过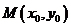 的抛物线的切线方程为
的抛物线的切线方程为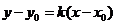
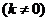 ,代入
,代入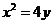 ,消去
,消去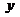 ,得
,得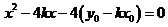
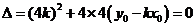 即:
即: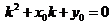 .................5分
.................5分
从而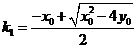 ,
,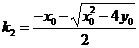 此时
此时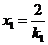 ,
,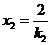
所以切点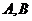 的坐标分别为
的坐标分别为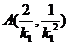 ,
,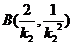 .................6分
.................6分
因为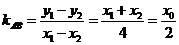 ,
,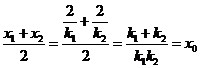 ,
,
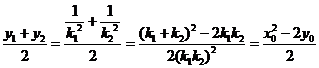 ,
,
所以 的中点坐标为
的中点坐标为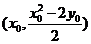
故直线 的方程为
的方程为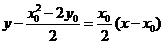 ,即
,即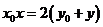 ...............7分
...............7分
又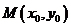 为直线
为直线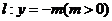 上任意一点,故
上任意一点,故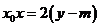 对任意
对任意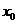 成立,所以
成立,所以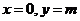 ,从而直线
,从而直线 恒过定点
恒过定点 ..................8分
..................8分
证法三:由已知得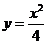 ,求导得
,求导得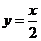 ,切点分别为
,切点分别为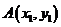 ,
,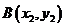 ,故过点
,故过点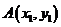 的切线斜率为
的切线斜率为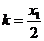 ,从而切线方程为
,从而切线方程为 即
即
又切线过点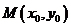 ,所以得
,所以得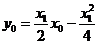 ① 即
① 即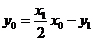
同理可得过点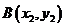 的切线为
的切线为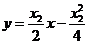 ,
,
又切线过点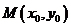 ,所以得
,所以得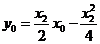 ②
②
即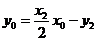 .................6分
.................6分
即点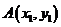 ,
,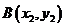 均满足
均满足 即
即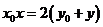 ,故直线
,故直线 的方程为
的方程为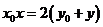 .................7分
.................7分
又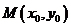 为直线
为直线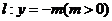 上任意一点,故
上任意一点,故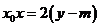 对任意
对任意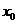 成立,所以
成立,所以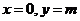 ,从而直线
,从而直线 恒过定点
恒过定点 ..................8分
..................8分
(3)解法一:由(2)中①②两式知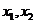 是方程
是方程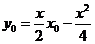 的两实根,故有
的两实根,故有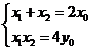
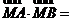
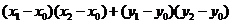
 (*)
(*)
将 ,
,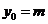 ,代入上(*)式得
,代入上(*)式得
∴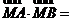
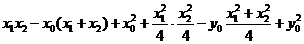
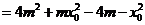
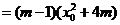 , .................9分
, .................9分
①当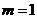 时,
时,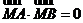 ,直线
,直线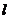 上任意一点
上任意一点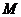 均有
均有 ,
,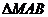 为直角三角形;
.................10分
为直角三角形;
.................10分
②当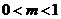 时,
时,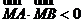 ,
,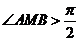 ,
,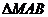 不可能为直角三角形;
不可能为直角三角形;
.................11分
③当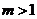 时,
时,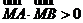 ,
,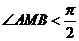 .
.
因为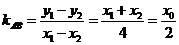 ,
,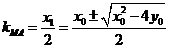 ,
,
所以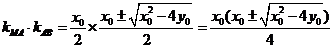
若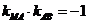 ,则
,则 ,整理得
,整理得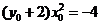 ,
,
又因为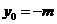 ,所以
,所以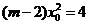 ,
,
因为方程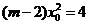 有解的充要条件是
有解的充要条件是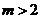 .
.
所以当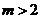 时,有
时,有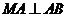 或
或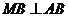 ,
,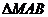 为直角三角形..............13分
为直角三角形..............13分
综上所述,当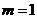 时,直线
时,直线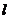 上任意一点
上任意一点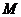 ,使
,使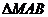 为直角三角形,当
为直角三角形,当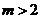 时,直线
时,直线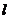 上存在两点
上存在两点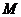 ,使
,使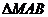 为直角三角形;当
为直角三角形;当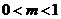 或
或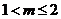 时,
时,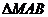 不是直角三角形.
不是直角三角形.
.................14分
解法二:由(2)知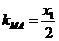 ,
,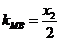 且
且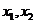 是方程
是方程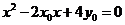 的两实根,即
的两实根,即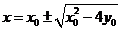 ,从而
,从而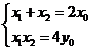 ,
,
所以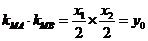
当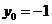 时,即
时,即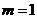 时,直线
时,直线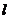 上任意一点
上任意一点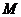 均有
均有 ,
,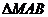 为直角三角形;
.................10分
为直角三角形;
.................10分
当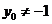 时,即
时,即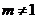 时,
时, 与
与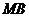 不垂直。
不垂直。
因为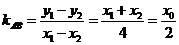 ,
,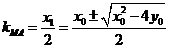 ,
,
所以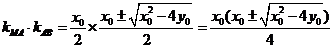
若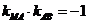 ,则
,则 ,整理得
,整理得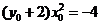 ,
,
又因为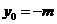 ,所以
,所以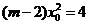 ,
,
因为方程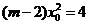 有解的充要条件是
有解的充要条件是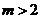 .
.
所以当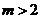 时,有
时,有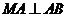 或
或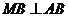 ,
,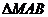 为直角三角形..............13分
为直角三角形..............13分
综上所述,当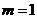 时,直线
时,直线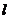 上任意一点
上任意一点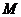 ,使
,使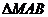 为直角三角形,当
为直角三角形,当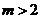 时,直线
时,直线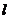 上存在两点
上存在两点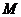 ,使
,使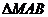 为直角三角形;当
为直角三角形;当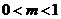 或
或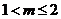 时,
时,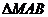 不是直角三角形.
不是直角三角形.
.................14分

 (2013•浙江模拟)如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于( )
(2013•浙江模拟)如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于( )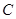 的方程为
的方程为 ,
, 为直线
为直线 上任意一点,过点
上任意一点,过点 ,切点分别为
,切点分别为 ,
, .
. 时,求过
时,求过 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线 与此圆的位置关系;
与此圆的位置关系;
 恒过定点;
恒过定点; 变化时,试探究直线
变化时,试探究直线 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.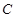 的方程为
的方程为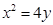 ,
,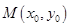 为直线
为直线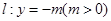 上任意一点,过点
上任意一点,过点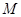 作抛物线
作抛物线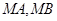 ,切点分别为
,切点分别为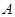 ,
,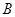 .
. 时,求过
时,求过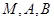 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线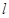 与此圆的位置关系;
与此圆的位置关系;
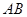 恒过定点
恒过定点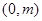 .
.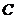 的方程为
的方程为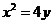 ,
, 为直线
为直线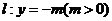 上任意一点,过点
上任意一点,过点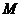 作抛物线
作抛物线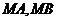 ,切点分别为
,切点分别为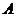 ,
,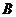 .
.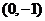 时,求过
时,求过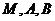 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线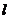 与此圆的位置关系;
与此圆的位置关系; 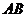 恒过定点
恒过定点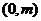 .
.