摘要:20.在平面直角坐标系中.已知A1.A2.P().M.O为坐标原点.若实数使向量.和满足. (1)求点P的轨迹方程.并判断P点的轨迹是怎样的曲线, (2)当时.过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B.能否在直线上找到一点C.恰使为正三角形?请说明理由. [解答](1)由已知可得...且.∴即. 即点P的轨迹方程是. 当即时.有. 此时.∴.综合知此时点的轨迹即为两点A1和A2, 当即时.方程为. 此时点P的轨迹是双曲线, 当时.方程为.且为两条射线, (2)过点A1斜率为1的直线方程为. 当时.曲线方程为.其轨迹就是两点A1和A2. 此时直线过点A1但不过A2点.∴B点不存在.从而这样的三角形也不存在.
网址:http://m.1010jiajiao.com/timu3_id_517798[举报]
(本小题满分13分)
如图,已知 、
、 为平面上的两个定点
为平面上的两个定点 ,
, ,且
,且 ,
, (
( 为动点,
为动点, 是
是 和
和 的交点).
的交点).
(Ⅰ)建立适当的平面直角坐标系求出点 的轨迹方程;
的轨迹方程;
(Ⅱ)若点 的轨迹上存在两个不同的点
的轨迹上存在两个不同的点 、
、 ,且线段
,且线段 的中垂线与直线
的中垂线与直线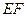 相交于一点
相交于一点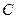 ,证明
,证明 <
< (
( 为
为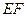 的中点).
的中点).
 中,O为坐标原点,已知点A
中,O为坐标原点,已知点A
 求证:
求证: ;
; 求
求 的值.
的值. 中,O为坐标原点,已知点A
中,O为坐标原点,已知点A
 求证:
求证: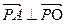 ;
; 求
求 的值.
的值. (Ⅱ)若点
(Ⅱ)若点 、
、 为平面上的两个定点
为平面上的两个定点 ,
,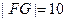 ,且
,且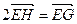 ,
,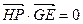 (
(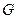 为动点,
为动点,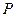 是
是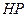 和
和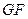 的交点).
的交点).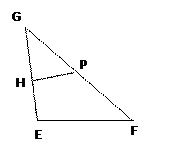
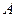 、
、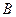 ,且线段
,且线段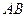 的中垂线与直线
的中垂线与直线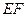 相交于一点
相交于一点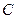 ,证明
,证明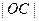 <
<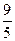 (
(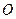 为
为