题目内容
(本小题满分13分)
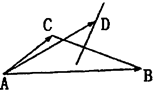
如图,已知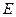 、
、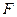 为平面上的两个定点
为平面上的两个定点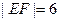 ,
,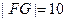 ,且
,且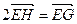 ,
,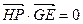 (
(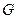 为动点,
为动点,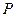 是
是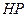 和
和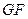 的交点).
的交点).
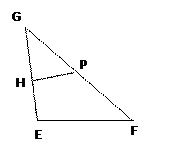
(Ⅰ)建立适当的平面直角坐标系求出点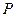 的轨迹方程;
的轨迹方程;
(Ⅱ)若点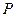 的轨迹上存在两个不同的点
的轨迹上存在两个不同的点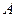 、
、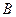 ,且线段
,且线段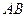 的中垂线与直线
的中垂线与直线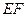 相交于一点
相交于一点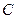 ,证明
,证明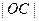 <
<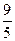 (
(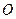 为
为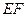 的中点).
的中点).
如图,已知
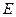 、
、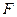 为平面上的两个定点
为平面上的两个定点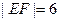 ,
,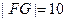 ,且
,且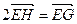 ,
,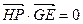 (
(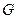 为动点,
为动点,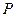 是
是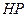 和
和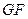 的交点).
的交点).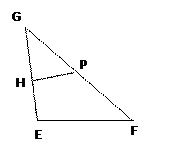
(Ⅰ)建立适当的平面直角坐标系求出点
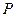 的轨迹方程;
的轨迹方程;(Ⅱ)若点
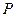 的轨迹上存在两个不同的点
的轨迹上存在两个不同的点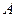 、
、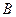 ,且线段
,且线段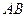 的中垂线与直线
的中垂线与直线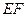 相交于一点
相交于一点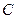 ,证明
,证明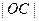 <
<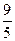 (
(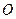 为
为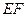 的中点).
的中点).解:(Ⅰ)以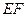 所在的直线为
所在的直线为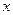 轴,
轴,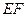 的中垂线为
的中垂线为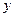 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
由题设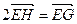 ,
,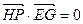 ,
,
∴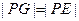 ,而
,而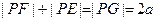 .
.
∴点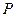 是以
是以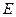 、
、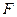 为焦点、长轴长为10的椭圆.
为焦点、长轴长为10的椭圆.
故点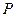 的轨迹方程是
的轨迹方程是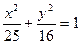 .…………………………………(4分)
.…………………………………(4分)
(Ⅱ)设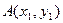 ,
,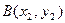 ,
,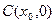 .
.
∴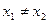 ,且
,且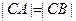 ,即
,即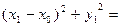
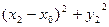 .
.
又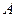 、
、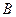 在轨迹上,∴
在轨迹上,∴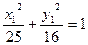 ,
,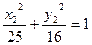 .
.
即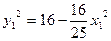 ,
,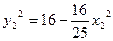 .
.
代入整理,得
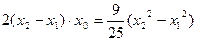 .
.
∵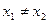 ,∴
,∴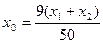 .
.
∵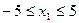 ,
,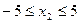 ,∴
,∴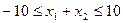 .
.
∵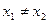 ,∴
,∴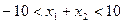 .
.
∴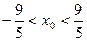 ,即
,即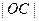 <
<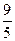 .……………………………………………(13分)
.……………………………………………(13分)
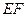 所在的直线为
所在的直线为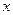 轴,
轴,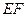 的中垂线为
的中垂线为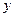 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.由题设
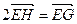 ,
,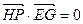 ,
,∴
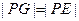 ,而
,而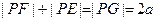 .
.∴点
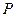 是以
是以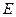 、
、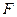 为焦点、长轴长为10的椭圆.
为焦点、长轴长为10的椭圆.故点
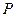 的轨迹方程是
的轨迹方程是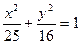 .…………………………………(4分)
.…………………………………(4分)(Ⅱ)设
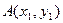 ,
,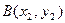 ,
,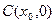 .
.∴
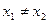 ,且
,且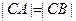 ,即
,即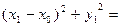
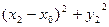 .
.又
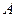 、
、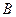 在轨迹上,∴
在轨迹上,∴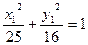 ,
,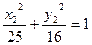 .
.即
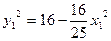 ,
,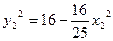 .
.代入整理,得
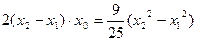 .
.∵
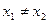 ,∴
,∴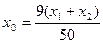 .
.∵
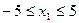 ,
,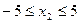 ,∴
,∴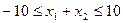 .
.∵
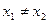 ,∴
,∴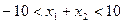 .
.∴
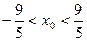 ,即
,即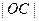 <
<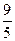 .……………………………………………(13分)
.……………………………………………(13分)略

练习册系列答案
相关题目

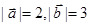 且
且 则
则 的值是( )
的值是( )




 为非零向量,“函数
为非零向量,“函数 为偶函数”是“
为偶函数”是“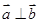 ”的
”的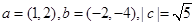 ,若
,若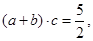
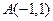 ,
,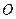 是坐标原点,点
是坐标原点,点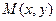 的坐标满足
的坐标满足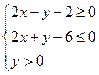 ,则
,则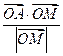 的取值范围是________.
的取值范围是________.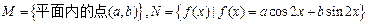 ,给出
,给出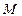 到
到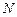 的映射
的映射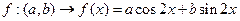 ,若点
,若点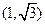 的像
的像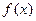 的图象可以由曲线
的图象可以由曲线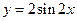 按向量m平移得到,则向量m的坐标为
按向量m平移得到,则向量m的坐标为 B.
B. C.
C. D.
D.
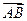 |=3,|
|=3,|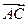 |=1,D是BC边中垂线上任意一点,则
|=1,D是BC边中垂线上任意一点,则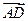 ·(
·(