摘要:直线方程及其应用 [教学要求]1. 理解直线斜率的概念.掌握过两点的直线的斜率公式.掌握直线方程的点斜式.两点式.一般式.并能根据条件熟练求出直线方程.
网址:http://m.1010jiajiao.com/timu3_id_517546[举报]
给出命题:
①线性回归分析就是由样本点去寻找一条贴近这些点的直线;
②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;
③通过回归方程
=bx+a及其回归系数b可以估计和预测变量的取值和变化趋势;
④线性相关关系就是两个变量间的函数关系.其中正确的命题是( )
①线性回归分析就是由样本点去寻找一条贴近这些点的直线;
②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;
③通过回归方程
| ? |
| y |
④线性相关关系就是两个变量间的函数关系.其中正确的命题是( )
| A、①② | B、①④ |
| C、①②③ | D、①②③④ |
在国庆60周年前夕,我市物价部门对本市五个商场销售的某件商品一天的销售量及其价格进行调查.五个商场的售价x元和销售量y件之间的一组数据如表:通过分析,发现销售量y对商品的价格x具有线性相关关系,那么销售量y对商品价格x的回归直线方程为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
在2010年3月15日那天,哈市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归直线方程是;y=-3.2x+a,(参考公式:回归方程;y=bx+a,a=
-b
),则a=( )
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
| y |
| x |
| A、-24 | B、35.6 |
| C、40.5 | D、40 |
在2013年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
 ,那么
,那么 的值为 ( )
的值为 ( )A.-24 B.35.6 C.40.5 D.40 查看习题详情和答案>>
在2013年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
|
价格x |
9 |
9.5 |
10 |
10.5 |
11 |
|
销售量y |
11 |
10 |
8 |
6 |
5 |
由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归直线方程是: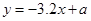 ,那么
,那么 的值为 ( )
的值为 ( )
A.-24 B.35.6 C.40.5 D.40
查看习题详情和答案>>
