题目内容
在2013年3月15日，某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查，5家商场的售价x元和销售量y件之间的一组数据如下表所示：
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
，那么
的值为 ( )A．－24 B．35.6 C．40.5 D．40
D
解析试题分析：线性回归方程过样本点中心，根据表中数据可得样本点中心为
，代入回归方程可以求出的值为40.
考点：本小题主要考查回归直线方程的应用.
点评：线性回归方程过样本点中心，这一性质经常考查，要灵活运用.
练习册系列答案
相关题目
废品率x%和每吨生铁成本y（元）之间的回归直线方程为y=256+3x,表明（ ）
| A．废品率每增加1%，生铁成本增加259元. | B．废品率每增加1%，生铁成本增加3元. |
| C．废品率每增加1%，生铁成本每吨增加3元. | D．废品率不变，生铁成本为256元. |
为了解儿子身高与其父亲身高的关系，随机抽取5对父子身高数据如下
| 父亲身高x（cm） | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y（cm） | 175 | 175 | 176 | 177 | 177 |
A．
B．
C．
D．
样本点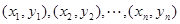
的样本中心与回归直线
的关系（ ）
| A．在直线上 | B．在直线左上方 | C．在直线右下方 | D．在直线外 |
随机变量
的观测值
越大，说明两个分类变量之间没有关系的可能性（ ）
| A．越大 | B．越小 | C．不变 | D．无法确定 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量160,则中间一组的频数为
| A．32 | B．0.2 | C．40 | D．0.25 |
某单位有老年人27 人，中年人54人，青年人81人，为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为36样本，则老年人、中年人、青年人分别各
抽取的人数是 ( )
| A．6，12，18 | B．7，11，19 | C．6，13，17 | D．7，12，17 |
，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取（ ） 名学生一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了8次试验，收集数据如下：
| 零件个数x（个） | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 加工时间y（分钟） | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 |
，则点
在直线
的（ ）A、右上方 B、右下方 C、左上方 D、左下方