摘要：(一)选择题 1.方程表示的曲线是 A. 椭圆 B.双曲线 C.抛物线 D.不能确定 2.把椭圆绕它的左焦点顺时针方向旋转.则所得新椭圆的准线方程是 A. B. C. D. 3.方程的曲线形状是 A.圆 B.直线 C.圆或直线 D.圆或两射线 4.F1.F2是椭圆的两焦点.过F1的弦AB与F2组成等腰直角三角形ABF2.其中∠BAF2=900.则椭圆的离心率是 A. B. C. D. 5.若方程表示焦点在y轴上的双曲线.则它的半焦距C的取值范围是 A. C. D.与m有关 6.以抛物线y2=2px的焦半径|PF|为直径的圆与y轴位置关系是 A.相交 B.相切 C.相离 D.以上三种均有可能 7.直线y=kx-2交抛物线y2=8x于A.B两点.若AB中点横坐标为2.则|AB|为 A. B. C. D. 8.已知圆x2+y2=1.点A(1.0).△ABC内接于圆.∠BAC=600.当BC在圆上运动时.BC中点的轨迹方程是 A.x2+y2= B.x2+y2= C.x2+y2= D.x2+y2=
网址：http://m.1010jiajiao.com/timu3_id_516411[举报]
已知
之间满足
（1）方程表示的曲线经过一点
，求b的值
（2）动点(x,y)在曲线
(b>0)上变化，求x2+2y的最大值；
（3）由能否确定一个函数关系式
，如能，求解析式；如不能，再加什么条件就可使之间建立函数关系，并求出解析式。
（
查看习题详情和答案>>.给出下列四个命题：
（1）方程
表示的是圆；
（2）动点到两个定点的距离之和为定长，则动点的轨迹为椭圆；
（3）点M与点F(0,-2)的距离比它到直线
的距离小1的
轨迹方程是
（4）若双曲线
的离心率为e，且
，则k的取值范围是
其中正确命题的序号是__________
查看习题详情和答案>>
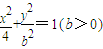
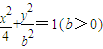表示的曲线经过一点
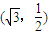，求b的值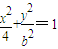
（b＞0）上变化，求x2+2y的最大值；
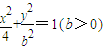能否确定一个函数关系式y=f（x），如能，求解析式；如不能，再加什么条件就可使x、y之间建立函数关系，并求出解析式．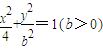
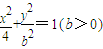表示的曲线经过一点
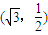，求b的值
（b＞0）上变化，求x2+2y的最大值．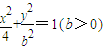
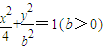表示的曲线经过一点
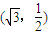，求b的值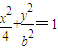
（b＞0）上变化，求x2+2y的最大值；
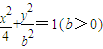能否确定一个函数关系式y=f（x），如能，求解析式；如不能，再加什么条件就可使x、y之间建立函数关系，并求出解析式．