摘要:8.(北师大版第132页A组第4题)两角和与差及二倍角的三角函数 已知..求.的值. 变式1:在中.已知... (Ⅰ)求的值, (Ⅱ)求的值. (Ⅰ)解:在中.. 由正弦定理. . 所以. (Ⅱ)解:因为.所以角为钝角.从而角为锐角. 于是. . . ∴ . 变式2:在中... (Ⅰ)求角的大小, (Ⅱ)若最大边的边长为.求最小边的边长. 解:(Ⅰ). . 又.. (Ⅱ). 边最大.即. 又. 角最小.边为最小边. 由且. 得.由得:. 所以最小边. 变式3:已知.且, (Ⅰ)求的值, (Ⅱ)求. 解:(Ⅰ)由.得 ∴.于是 (Ⅱ)由.得 又∵.∴ 由得: 所以.
网址:http://m.1010jiajiao.com/timu3_id_516265[举报]
阅读下面材料:
根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
α+β=A,α-β=B 有α=
,β=
代入③得 sinA+cosB=2sin
cos
.
(1)类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(2)若△ABC的三个内角A,B,C满足cos2A+cox2C-cos2B=1,直接利用阅读材料及(1)中的结论试判断△ABC的形状.
查看习题详情和答案>>
根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
α+β=A,α-β=B 有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+cosB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(1)类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(2)若△ABC的三个内角A,B,C满足cos2A+cox2C-cos2B=1,直接利用阅读材料及(1)中的结论试判断△ABC的形状.
阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
,β=
代入③得 sinA+subB=2sin
cos
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看习题详情和答案>>
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+subB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
(2012•福建模拟)阅读下面材料:
根据两角和与差的正弦公式,有sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=B有α=
,β=
代入③得 sinA+sinB=2sin
cos
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=2sin2C,试判断△ABC的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看习题详情和答案>>
根据两角和与差的正弦公式,有sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=B有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=2sin2C,试判断△ABC的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
阅读下面材料:
根据两角和与差的正弦公式,有:
sin(α+β)=sinαcosβ+cosαsinβ…①
sin(α-β)=sinαcosβ-cosαsinβ…②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ…③
令α+β=A,α-β=B有α=
,β=
代入③得sinA+sinB=2sin
cos
.
(Ⅰ)类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=1-cos2C,试判断△ABC的形状.(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看习题详情和答案>>
根据两角和与差的正弦公式,有:
sin(α+β)=sinαcosβ+cosαsinβ…①
sin(α-β)=sinαcosβ-cosαsinβ…②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ…③
令α+β=A,α-β=B有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ)类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=1-cos2C,试判断△ABC的形状.(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
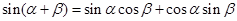 ------①
------①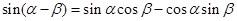 ------②
------②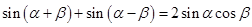 ------③
------③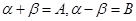 有
有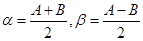
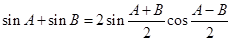 .
.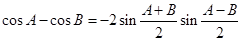 ;
;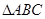 的三个内角
的三个内角 满足
满足 ,直接利用阅读材料及(1)中的结论试判断
,直接利用阅读材料及(1)中的结论试判断