摘要:已知函数f(x)满足f(logax)= (其中a>0,a≠1,x>0),求f(x)的表达式 解 (1)令t=logax(a>1.t>0,0<a<1.t<0).则x=at 因此f(t)= (at-a-t) ∴f(x)= (ax-a-x)(a>1,x>0;0<a<1,x<0) 10已知函数的图象在点M(-1.f(x))处的切线方程为x+2y+5=0. (Ⅰ)求函数y=f(x)的解析式,(Ⅱ)求函数y=f(x)的单调区间. 解:(1)由函数f(x)的图象在点M(-1f(-1))处的 切线方程为x+2y+5=0.知
网址:http://m.1010jiajiao.com/timu3_id_516056[举报]
已知函数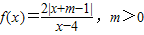 ,满足f(2)=-2,
,满足f(2)=-2,
(1)求实数m的值;
(2)判断y=f(x)在区间(-∞,m-1]上的单调性,并用单调性定义证明;
(3)若关于x的方程f(x)=kx有三个不同实数解,求实数k的取值范围.
查看习题详情和答案>>
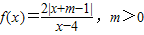 ,满足f(2)=-2,
,满足f(2)=-2,(1)求实数m的值;
(2)判断y=f(x)在区间(-∞,m-1]上的单调性,并用单调性定义证明;
(3)若关于x的方程f(x)=kx有三个不同实数解,求实数k的取值范围.
查看习题详情和答案>>
已知函数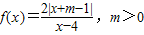 ,满足f(2)=-2,
,满足f(2)=-2,
(1)求实数m的值;
(2)判断y=f(x)在区间(-∞,m-1]上的单调性,并用单调性定义证明;
(3)若关于x的方程f(x)=kx有三个不同实数解,求实数k的取值范围.
查看习题详情和答案>>
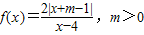 ,满足f(2)=-2,
,满足f(2)=-2,(1)求实数m的值;
(2)判断y=f(x)在区间(-∞,m-1]上的单调性,并用单调性定义证明;
(3)若关于x的方程f(x)=kx有三个不同实数解,求实数k的取值范围.
查看习题详情和答案>>
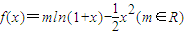 ,满足f′(0)=1.
,满足f′(0)=1.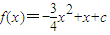 在[0,2]恰有两个不同的实根,求实数c的取值范围.
在[0,2]恰有两个不同的实根,求实数c的取值范围.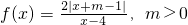 ,满足f(2)=-2,
,满足f(2)=-2,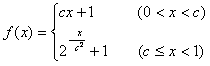 ,满足f(c2)=
,满足f(c2)=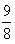 ,
, 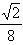 +1。
+1。