题目内容
已知函数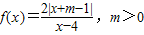 ,满足f(2)=-2,
,满足f(2)=-2,(1)求实数m的值;
(2)判断y=f(x)在区间(-∞,m-1]上的单调性,并用单调性定义证明;
(3)若关于x的方程f(x)=kx有三个不同实数解,求实数k的取值范围.
【答案】分析:(1)利用f(2)=-2即m>0即可求出;
(2)利用(1)先求出其解析式及单调区间,再利用定义证明即可;
(3)通过对x分别就x>0、x=0、x<0三种情况的解的情况讨论即可.
解答:解:(1)由f(2)=-2,m>0⇒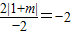 ,m>0,解得m=1.
,m>0,解得m=1.
(2)由(1)可知:m=1,∴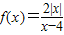 .
.
因此只研究函数f(x)=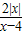 =
=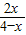 在区间(-∞,0]上的单调性即可.
在区间(-∞,0]上的单调性即可.
此函数在区间(-∞,0]上单调递增.
证明:设x1<x2≤0,
则f(x1)-f(x2)=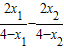 =
=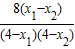 ,
,
∵x1<x2≤0,∴x1-x2<0,4-x1>0,4-x2>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)在(-∞,0]上单调递增.
(3)原方程即为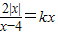 (*)
(*)
①当x=0时,方程成立,即x=0是方程(*)的一个实数根;
②当x<0时,方程(*)?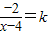 ,x<0?
,x<0?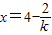 <0?
<0?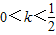 ,
,
即当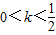 时,方程(*)在区间(-∞,0)有唯一一个实数根,此外无解;
时,方程(*)在区间(-∞,0)有唯一一个实数根,此外无解;
③当x>0且x≠4时,方程(*)? ,x>0且x≠4?x=
,x>0且x≠4?x=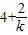 >0,解得
>0,解得 或k>0.
或k>0.
∴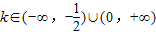 时,方程(*)在区间(0,+∞)有一个实数根,此外无解.
时,方程(*)在区间(0,+∞)有一个实数根,此外无解.
综上可知:要使原方程有三个不同实数根,当且仅当k满足原方程在(-∞,0)和(0,+∞)
各有一个实数解时才成立,此时,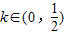 .
.
∴实数k的取值范围为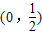 .
.
点评:熟练掌握函数的单调性和分类讨论的思想方法是解题的关键.
(2)利用(1)先求出其解析式及单调区间,再利用定义证明即可;
(3)通过对x分别就x>0、x=0、x<0三种情况的解的情况讨论即可.
解答:解:(1)由f(2)=-2,m>0⇒
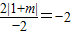 ,m>0,解得m=1.
,m>0,解得m=1.(2)由(1)可知:m=1,∴
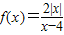 .
.因此只研究函数f(x)=
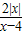 =
=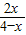 在区间(-∞,0]上的单调性即可.
在区间(-∞,0]上的单调性即可.此函数在区间(-∞,0]上单调递增.
证明:设x1<x2≤0,
则f(x1)-f(x2)=
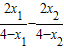 =
=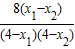 ,
,∵x1<x2≤0,∴x1-x2<0,4-x1>0,4-x2>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)在(-∞,0]上单调递增.
(3)原方程即为
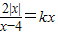 (*)
(*)①当x=0时,方程成立,即x=0是方程(*)的一个实数根;
②当x<0时,方程(*)?
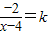 ,x<0?
,x<0?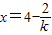 <0?
<0?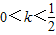 ,
,即当
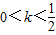 时,方程(*)在区间(-∞,0)有唯一一个实数根,此外无解;
时,方程(*)在区间(-∞,0)有唯一一个实数根,此外无解;③当x>0且x≠4时,方程(*)?
 ,x>0且x≠4?x=
,x>0且x≠4?x=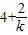 >0,解得
>0,解得 或k>0.
或k>0.∴
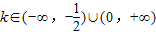 时,方程(*)在区间(0,+∞)有一个实数根,此外无解.
时,方程(*)在区间(0,+∞)有一个实数根,此外无解.综上可知:要使原方程有三个不同实数根,当且仅当k满足原方程在(-∞,0)和(0,+∞)
各有一个实数解时才成立,此时,
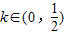 .
.∴实数k的取值范围为
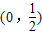 .
.点评:熟练掌握函数的单调性和分类讨论的思想方法是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
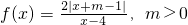 ,满足f(2)=-2,
,满足f(2)=-2,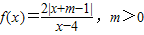 ,满足f(2)=-2,
,满足f(2)=-2,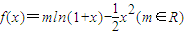 ,满足f′(0)=1.
,满足f′(0)=1.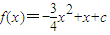 在[0,2]恰有两个不同的实根,求实数c的取值范围.
在[0,2]恰有两个不同的实根,求实数c的取值范围.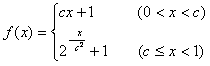 ,满足f(c2)=
,满足f(c2)=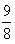 ,
, 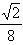 +1。
+1。