摘要:43.已知的前n项之和-的值为 ( ) A.67 B.65 C.61 D.55 正确答案:A 错误原因:认为为等差数列.实质为 二填空题:
网址:http://m.1010jiajiao.com/timu3_id_514903[举报]
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f-1(x)能确定数列{bn},bn=f-1(n),若对于任意n?N*,都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(1)若函数f(x)=
确定数列{an}的自反数列为{bn},求an;
(2)在(1)条件下,记
为正数数列{xn}的调和平均数,若dn=
-1,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求
=
;
(3)已知正数数列{cn}的前n项之和Tn=
(Cn+
).求Tn表达式.
查看习题详情和答案>>
(1)若函数f(x)=
| px+1 |
| x+1 |
(2)在(1)条件下,记
| n | ||||||
|
| 2 |
| an+1 |
| lim |
| n→∞ |
| Hn |
| n |
(3)已知正数数列{cn}的前n项之和Tn=
| 1 |
| 2 |
| n |
| Cn |
(文)已知无穷等比数列{an}中,首项a1=1000,公比q=
;数列{bn}满足bn=
(lga1+lga2+…+lgan).求:
(1)无穷等比数列{an}各项的和;
(2)数列{bn}的通项公式;
(3)数列{bn}的前n项之和的最大值. 查看习题详情和答案>>
| 1 |
| 10 |
| 1 |
| n |
(1)无穷等比数列{an}各项的和;
(2)数列{bn}的通项公式;
(3)数列{bn}的前n项之和的最大值. 查看习题详情和答案>>
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f-1(x)能确定数列{bn},bn=f-1(n),若对于任意nÎN*,都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(1)若函数f(x)=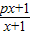 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;
(2)在(1)条件下,记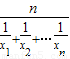 为正数数列{xn}的调和平均数,若dn=
为正数数列{xn}的调和平均数,若dn=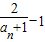 ,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求
,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求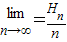 ;
;
(3)已知正数数列{cn}的前n项之和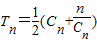 .求Tn表达式.
.求Tn表达式.
查看习题详情和答案>>
(1)若函数f(x)=
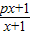 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;(2)在(1)条件下,记
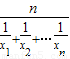 为正数数列{xn}的调和平均数,若dn=
为正数数列{xn}的调和平均数,若dn=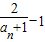 ,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求
,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求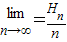 ;
;(3)已知正数数列{cn}的前n项之和
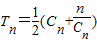 .求Tn表达式.
.求Tn表达式.查看习题详情和答案>>
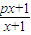 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;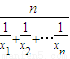 为正数数列{xn}的调和平均数,若dn=
为正数数列{xn}的调和平均数,若dn=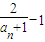 ,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求
,Sn为数列{dn}的前n项之和,Hn为数列{Sn}的调和平均数,求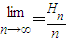 ;
;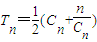 .求Tn表达式.
.求Tn表达式.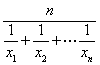 为正数数列{xn}的调和平均数,若dn=
为正数数列{xn}的调和平均数,若dn=