题目内容
由函数y=f（x）确定数列{an}，an=f（n），函数y=f（x）的反函数y=f –1（x）能确定数列{bn}，bn= f –1（n），若对于任意nÎN*，都有bn=an，则称数列{bn}是数列{an}的“自反数列”．
（1）若函数f（x）=
确定数列{an}的自反数列为{bn}，求an；
（2）在（1）条件下，记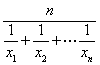
为正数数列{xn}的调和平均数，若dn=
，Sn为数列{dn}的前n项之和，Hn为数列{Sn}的调和平均数，求
；
（3）已知正数数列{cn}的前n项之和
求Tn表达式．
解：（1）由题意的：f –1（x）=
= f（x）=，所以p =－1，…………2分
所以an=
………………………………………………………………………3分翰林汇
（2）an=，
，…………………………………………4分
为数列{dn}的前n项和，
，……………………………………5分
又Hn为数列{Sn}的调和平均数，
所以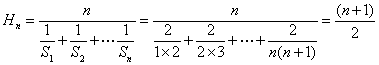
………8分
………………………………………………………10分
（3）因为正数数列{cn}的前n项之和
所以
解之得：c1=1，T1=1……………………………………11分
当
……………………………………14分
所以，
累加得：
………………………………………………16分
…………………18分
练习册系列答案
相关题目