题目内容
(文)已知无穷等比数列{an}中,首项a1=1000,公比q=| 1 |
| 10 |
| 1 |
| n |
(1)无穷等比数列{an}各项的和;
(2)数列{bn}的通项公式;
(3)数列{bn}的前n项之和的最大值.
分析:(1)利用无穷等比数列的求和公式即可求得{an}各项的和;
(2)由lgan=4-n,可知lgan为等差数列,利用其求和公式可求得bn;
(3)由bn=
,可以求得其前n项和的表达式,从而可求其最大值.
(2)由lgan=4-n,可知lgan为等差数列,利用其求和公式可求得bn;
(3)由bn=
| 7-n |
| 2 |
解答:解:(1)S=
=
; …(4分)
(2)lgan=4-n,bn=
(lga1+lga2+…+lgan)=
=
; …(8分)
(3)设数列{bn}的前n项之和为Tn,则Tn=
,…(12分)
当n=6,7时,Tn取得最大值
.…(16分)
| a1 |
| 1-q |
| 10000 |
| 9 |
(2)lgan=4-n,bn=
| 1 |
| n |
| 3+4-n |
| 2 |
| 7-n |
| 2 |
(3)设数列{bn}的前n项之和为Tn,则Tn=
| -n2+13n |
| 4 |
当n=6,7时,Tn取得最大值
| 21 |
| 2 |
点评:本题考查数列求和,重点考查学生无穷等比数列与等差数列的求和公式,着重配方法的考查,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 ,各项的和
,各项的和 ,则
公比q=_______________
,则
公比q=_______________ ;数列{bn}满足
;数列{bn}满足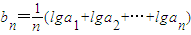 .求:
.求: