摘要： 设等差数列{an}的首项为a.公差为2a.前n项和为Sn.记A={(x.y)|x=n.y=.n∈N*}.B={2+y2=1.x.y∈R}. (1)若A∩B≠ ?.求a的取值集合, (2)设点P∈A.点Q∈B.当a=时.求|PQ|的最小值.
网址：http://m.1010jiajiao.com/timu3_id_514433[举报]
本小题满分12分）
已知等差数列{an}的首项a1＝1，公差d＞0，且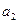
、
、
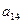分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设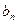
＝
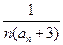（n∈N*），
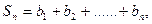求
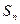
(本小题满分12分高☆考♂资♀源?网)
已知等差数列{an}的首项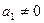
，前n项和为Sn，且S4+a2=2S3；等比数列{bn}满足b1=a2，b2=a4
（1）若a1=2，设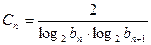
，求数列{cn}的前n项的和Tn；
（2）在（1）的条件下，若有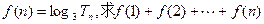
的最大值．
本小题满分12分）
已知等差数列{an}的首项a1＝1，公差d＞0，且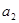
、
、
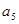分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设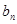
＝
（n∈N*），
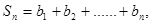求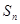
查看习题详情和答案>>
、
、
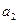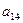分别是一个等比数列的第二项、第三项、第四项．
＝
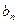（n∈N*），
求
12分）已知等差数列{an2
}中，首项a12＝1，公差d＝1，an＞0，n∈N
*．
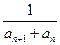，数列{bn}的前120项和T120；