摘要:18. 解:(1)设圆心为. --1分 因为圆与相切. 所以. 解得. ----3分 所以圆的方程为 ----4分 (2)显然直线的斜率存在.设直线的方程为. 由. ----5分 ∵直线与圆相交于不同两点 . ----6分 设.则 . ① . ----8分 将①代入并整理得. 解得或. 所以直线的方程为 ----10分 圆心到的距离. ----14分
网址:http://m.1010jiajiao.com/timu3_id_514101[举报]
求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程,首先
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2)
∴r= =
= ,
,
故所求圆的方程为: +
+ =2
=2
解:法一:
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2) ……………………8分
∴r= =
= ,
………………………10分
,
………………………10分
故所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
法二:由条件设所求圆的方程为: +
+ =
=
 , ………………………6分
, ………………………6分
解得a=1,b=-2,  =2
………………………10分
=2
………………………10分
所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
其它方法相应给分
查看习题详情和答案>>
 ,乙同学解出它的概率为
,乙同学解出它的概率为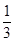 ,丙同学解出它的概率为
,丙同学解出它的概率为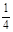 ,则独立解答此题时,三人中只有一人解出的概率为
,则独立解答此题时,三人中只有一人解出的概率为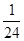 B.
B.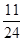 C.
C.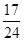 D.1
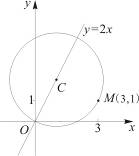
D.1 在直线
在直线 上,且经过原点及点
上,且经过原点及点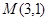 的圆
的圆 ),然后利用
),然后利用 ,得到
,得到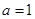 ,从而圆心
,从而圆心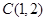 ,半径
,半径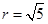 .可得原点 标准方程。
.可得原点 标准方程。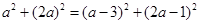 ,解得
,解得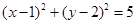 .......10分
.......10分