摘要:21. 设函数.其图象在点处的切线 的斜率分别为. (Ⅰ)求证:, (Ⅱ)若函数的递增区间为.求的取值范围, (Ⅲ)若当时(k是与无关的常数).恒有.试求k的最小值.
网址:http://m.1010jiajiao.com/timu3_id_513890[举报]
(本小题满分16分)已知函数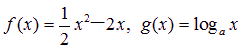 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果![]() 是增函数,且
是增函数,且![]() 存在零点(
存在零点(![]() 为
为![]() 的导函数).
的导函数).
(Ⅰ)求a的值;(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,![]() (
(![]() 为
为![]() 的导函数),证明:
的导函数),证明:![]() .
.
(本小题满分16分)
已知定义在实数集上的函数![]() ,其导函数记为
,其导函数记为![]() ,且满足
,且满足![]() ,
,![]() 为常数,
为常数,![]() .
.
(1)试求![]() 的值;
的值;
(2)记函数![]() ,
,![]() ,若
,若![]() 的最小值为6,求实数
的最小值为6,求实数![]() 的值;
的值;
(3)对于(2)中的![]() ,设函数
,设函数![]() ,
,![]() (
(![]() )是函数
)是函数![]() 图象上两点,若
图象上两点,若![]() ,试判断
,试判断![]() 的大小,并加以证明.
的大小,并加以证明.
(本小题满分16分)
设定义在区间[x1, x2]上的函数y=f(x)的图象为C,M是C上的任意一点,O为坐标原点,设向
量![]() =
=![]() ,
,![]() ,
,![]() =(x,y),当实数λ满足x=λ x1+(1-λ) x2时,记向
=(x,y),当实数λ满足x=λ x1+(1-λ) x2时,记向
量![]() =λ
=λ![]() +(1-λ)
+(1-λ)![]() .定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
.定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
“![]() k恒成立”,其中k是一个确定的正数.
k恒成立”,其中k是一个确定的正数.
(1)设函数 f(x)=x2在区间[0,1]上可在标准k下线性近似,求k的取值范围;
(2)求证:函数![]() 在区间
在区间![]() 上可在标准k=
上可在标准k=![]() 下线性近似.
下线性近似.
(参考数据:e=2.718,ln(e-1)=0.541)
查看习题详情和答案>>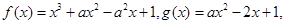 其中实数
其中实数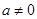 .
.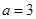 时,求函数
时,求函数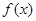 的单调区间;
的单调区间;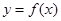 与
与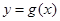 的图象只有一个公共点且
的图象只有一个公共点且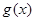 存在最小值时,
存在最小值时,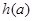 ,求函数
,求函数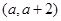 内均为增函数,求实数
内均为增函数,求实数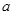 的取值范围.
的取值范围.