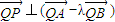摘要:9.如图.过抛物线x2=4y的对称轴上任一点P作直线与抛物线交于A,B两点.点Q是点P关于原点的对称点. (I)设点P分有向线段所成的比为.证明: (II)设直线AB的方程是x-2y+12=0.过A,B两点的圆C与抛物线在点A处有共同的切线.求圆C的方程.
网址:http://m.1010jiajiao.com/timu3_id_510067[举报]
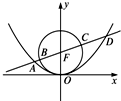
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.(I)若
| AP |
| PB |
| x1 |
| x2 |
(II)在(I)条件下,若点Q是点P关于原点对称点,证明:
| QP |
| QA |
| QB |
(III)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.(I)设点P分有向线段
| AB |
| QP |
| QA |
| QB |
(Ⅱ)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程. 查看习题详情和答案>>
 如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则
如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则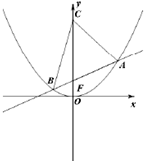 (2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
(2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).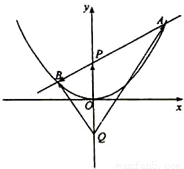 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.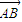 所成的比为λ,证明:
所成的比为λ,证明: