摘要：10．设二面角a―a―b的大小是60°.P是二面角内的一点.P点到a.b的距离分别为1cm. 2cm.那么点P到棱a的距离是 ( ) A． B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_509940[举报]
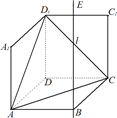如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A1和CD D′C1都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．（Ⅰ） 设二面角E-AC-D1的大小为θ，若
| π |
| 4 |
| π |
| 3 |
（Ⅱ）在线段D1E上存在点P，使平面PA1C1∥平面EAC，求
| D1P |
| PE |
| D1P |
| PE |
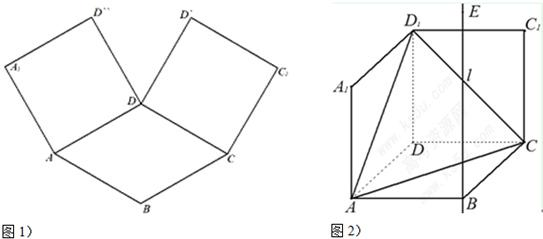
如图1，在平面内，ABCD是∠BAD=60°且AB=a的菱形，ADD''A1和CDD'C1都是正方形．将两个正方形分别沿AD，CD折起，使D''与D'重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧，设BE=t（t＞0）（图2）．
（1）设二面角E-AC-D1的大小为q，若
≤θ≤
，求t的取值范围；
（2）在线段D1E上是否存在点P，使平面PA1C1∥平面EAC，若存在，求出P分
所成的比λ；若不存在，请说明理由．
查看习题详情和答案>>
（1）设二面角E-AC-D1的大小为q，若
| π |
| 4 |
| π |
| 3 |
（2）在线段D1E上是否存在点P，使平面PA1C1∥平面EAC，若存在，求出P分
| D1E |
查看习题详情和答案>>
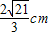
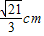
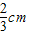
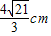
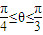，求t的取值范围；
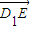所成的比λ；若不存在，请说明理由．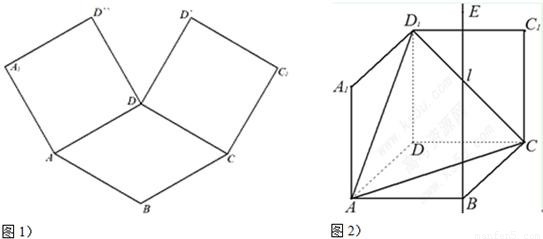
，求t的取值范围；
所成的比λ；若不存在，请说明理由．