题目内容
如图1,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADD''A1和CDD'C1都是正方形.将两个正方形分别沿AD,CD折起,使D''与D'重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设BE=t(t>0)(图2).(1)设二面角E-AC-D1的大小为q,若
| π |
| 4 |
| π |
| 3 |
(2)在线段D1E上是否存在点P,使平面PA1C1∥平面EAC,若存在,求出P分
| D1E |
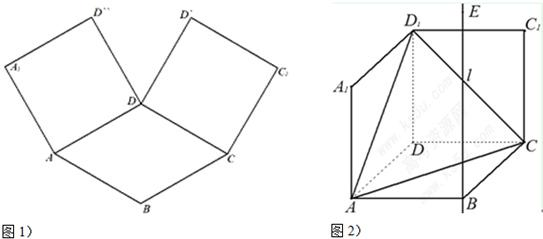
分析:(1)设菱形ABCD的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系,设BE=t,分别求出平面D1AC的法向量与平面EAC的法向量,代入向量夹角公式,根据
≤θ≤
,构造不等式,解不等式即可得到答案.
(2)假设存在满足题意的点P,令
=λ
,则可以求出P点的坐标,再根据平面PA1C1∥平面EAC,我们可根据
•
=0,构造方程,解方程即可求出满足条件的λ的值.
| π |
| 4 |
| π |
| 3 |
(2)假设存在满足题意的点P,令
| D1P |
| PE |
| A1P |
| n2 |
解答:解:(1)设菱形ABCD的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系如图.设BE=t(t>0).
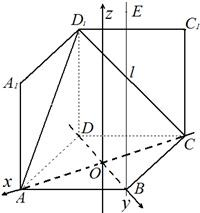
(1)A(
a,0,0),C(-
a,0,0),D1(0,-
,a),E(0,-
,t)
=(-
a,-
,a),
=(-
a,0,0)
设平面D1AC的法向量为
=(x1,y1,z1),
则
?
,
令z1=1得
=(0,2,1).
=(-
a,
,t),设平面EAC的法向量为
=(x2,y2,z2),
则
?
,
令z2=-a得
=(0,2t,-a).
设二面角E-AC-D1的大小为θ,则cosθ=
=
.
∵
≤θ≤
∴cosθ∈[
,
]
∴
≤|
|≤
解得
a≤t≤
所以t的取值范围是[
a,
].
(2)假设存在满足题意的点P,
令
=λ
则P(0,
•
,
)
由平面PA1C1∥平面EAC,
得A1P∥平面EAC,
∴
•
=0
∴t•
-
=0,
化简:λ=
(t≠a)
即线段D1E上存在点P,使平面PA1C1∥平面EAC,P分
所成的比λ=
(t≠a);

(1)A(
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
| AD1 |
| ||
| 2 |
| a |
| 2 |
| AC |
| 3 |
设平面D1AC的法向量为
| n1 |
则
|
|
令z1=1得
| n1 |
| AE |
| ||
| 2 |
| a |
| 2 |
| n2 |
则
|
|
令z2=-a得
| n2 |
设二面角E-AC-D1的大小为θ,则cosθ=
| ||||
|
|
| 4t-a | ||
|
∵
| π |
| 4 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| 4t-a | ||
|
| ||
| 2 |
解得
8+5
| ||
| 22 |
| 3a |
| 2 |
所以t的取值范围是[
8+5
| ||
| 22 |
| 3a |
| 2 |
(2)假设存在满足题意的点P,
令
| D1P |
| PE |
则P(0,
| a |
| 2 |
| λ-1 |
| λ+1 |
| λt+a |
| 1+λ |
由平面PA1C1∥平面EAC,
得A1P∥平面EAC,
∴
| A1P |
| n2 |
∴t•
| λ-1 |
| λ+1 |
| λt-aλ |
| 1+λ |
化简:λ=
| t |
| a |
即线段D1E上存在点P,使平面PA1C1∥平面EAC,P分
| D1E |
| t |
| a |
点评:本题考查的知识点是二面角的平面角及求法,民平面平行的判定,(1)的关键是出平面D1AC的法向量与平面EAC的法向量,代入向量夹角公式,根据
≤θ≤
,构造不等式,(2)的关键是根据
•
=0,构造方程.
| π |
| 4 |
| π |
| 3 |
| A1P |
| n2 |

练习册系列答案
相关题目
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
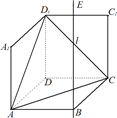 如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2). 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).

 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围; 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有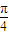 ≤θ≤
≤θ≤ ,求线段BE长的取值范围;
,求线段BE长的取值范围; 与BE之间满足的关系式,并证明:当0<BE<a时,恒有
与BE之间满足的关系式,并证明:当0<BE<a时,恒有 <1.
<1.