题目内容
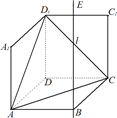 如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).(Ⅰ) 设二面角E-AC-D1的大小为θ,若
| π |
| 4 |
| π |
| 3 |
(Ⅱ)在线段D1E上存在点P,使平面PA1C1∥平面EAC,求
| D1P |
| PE |
| D1P |
| PE |
分析:(I)设菱形ABCD的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系BE=t,分别求出平面D1AC的法向量与平面EAC的法向量,代入向量夹角公式,并根据
≤θ≤
,构造关于t的不等式,即可求出线段BE长的取值范围;
(Ⅱ)设
=λ
,分别求出平面PA1C1和平面EAC的法向量,并根据平面PA1C1∥平面EAC得到λ,a,t的关系式,结合0<BE<a,即可得到结论.
| π |
| 4 |
| π |
| 3 |
(Ⅱ)设
| D1P |
| PE |
解答:解:设菱形ABCD的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系如图.
设BE=t(t>0).
(Ⅰ)A(
a,0,0),C(-
a,0,0),D1(0,-
,a),E(0,
,t).
=(-
a,-
,a),
=(-
a,0,0),
设平面D1AC的法向量为
=(x1,y1,1),则
?
?
∴
=(0,2,1).(3分)
=(-
a,
,t),
设平面EAC的法向量为
=(x2,y2,-1),
则
?
?
∴
=(0,
,-1).(4分)
设二面角E-AC-D1的大小为θ,则cosθ=
=
,(6分)
∵cosθ∈[
,
],∴
≤|
|≤
,
解得
a≤t≤
.所以BE的取值范围是[
a,
].(8分)
(Ⅱ)设
=λ
,则P(0,
•
,
).∵A1(
a,0,a),∴
=(-
a,
•
,
).
由平面PA1C1∥平面EAC,得A1P∥平面EAC,∴
•
=0.∴t•
-
=0,化简得:λ=
(t≠a),即所求关系式:
=
(BE≠a).
∴当0<t<a时,
<1.即:当0<BE<a时,恒有
<1.(14分)
设BE=t(t>0).
(Ⅰ)A(
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
| AD1 |
| ||
| 2 |
| a |
| 2 |
| AC |
| 3 |
设平面D1AC的法向量为
| n1 |
|
|
|
∴
| n1 |
| AE |
| ||
| 2 |
| a |
| 2 |
设平面EAC的法向量为
| n2 |
则
|
|
|
| n2 |
| 2t |
| a |
设二面角E-AC-D1的大小为θ,则cosθ=
| ||||
|
|
| 4t-a | ||
|
∵cosθ∈[
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 4t-a | ||
|
| ||
| 2 |
解得
8+5
| ||
| 22 |
| 3a |
| 2 |
8+5
| ||
| 22 |
| 3a |
| 2 |
(Ⅱ)设
| D1P |
| PE |
| a |
| 2 |
| λ-1 |
| λ+1 |
| λt+a |
| 1+λ |
| ||
| 2 |
| A1P |
| ||
| 2 |
| a |
| 2 |
| λ-1 |
| λ+1 |
| λt-aλ |
| 1+λ |
由平面PA1C1∥平面EAC,得A1P∥平面EAC,∴
| A1P |
| n2 |
| λ-1 |
| λ+1 |
| λt-aλ |
| 1+λ |
| t |
| a |
| D1P |
| PE |
| BE |
| a |
∴当0<t<a时,
| D1P |
| PE |
| D1P |
| PE |
点评:本题考查的知识点是用空间向量求平面间的夹角,平面与平面平行的性质,与二面角有关的立体几何综合问题,向量语言表述面面的平行关系,建立适当的空间坐标系,将空间二面角问题及面面平行问题转化为向量的夹角问题是解答本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
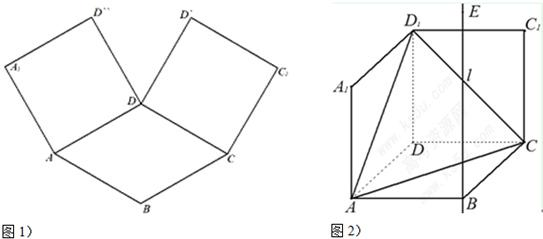
 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).

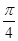 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围; 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有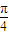 ≤θ≤
≤θ≤ ,求线段BE长的取值范围;
,求线段BE长的取值范围; 与BE之间满足的关系式,并证明:当0<BE<a时,恒有
与BE之间满足的关系式,并证明:当0<BE<a时,恒有 <1.
<1.