题目内容
试根据复合函数的求导法则,研究函数f(x)=xx(x>0)的性质,并回答:下列命题中假命题的个数是( )
①f(x)的极大值为1;
②f(x)的极小值为1;
③f(x)的一个单调递增区间是(
,10).
①f(x)的极大值为1;
②f(x)的极小值为1;
③f(x)的一个单调递增区间是(
| 1 |
| 10 |
| A、0 | B、1 | C、2 | D、3 |
分析:根据条件,对f(x)=xx=elnxx=exlnx,利用复合函数求导法则求出f′(x),令其等于0即可得到函数的单调区间与极值.
解答:解:∵f(x)=xx=elnxx=exlnx,
∴f′(x)=(xx)′=exlnx(lnx+1)=xx(lnx+1)=0
得x=

当x=
时,f(x)取极小值为e-
,
f(x)的单调递增区间是(
,+∞).
故命题①②③全错,
故选D.
∴f′(x)=(xx)′=exlnx(lnx+1)=xx(lnx+1)=0
得x=
| 1 |
| e |

当x=
| 1 |
| e |
| 1 |
| e |
f(x)的单调递增区间是(
| 1 |
| e |
故命题①②③全错,
故选D.
点评:本题考查对数的恒等变形,以及复合函数求导法则,利用导数研究函数的单调性和极值问题,考查了运算能力和分析解决问题的能力,以及计算能力,属中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
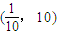 .
.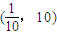 .
.