摘要:22..∵p.Q两点关于原点对称.∴p点的坐标为在函数y=f(x)的图象上.∴-y=loga=-loga ≥0得2loga(x+1)≥loga(1-x) ∵0<a<1 ∴-------------- (3)由题意知:a>1且x∈[0.1)时恒成立.----- 设.令t=1-x.t∈(0,1],∴ --------------------------------- 设 , ∴u(t)的最小值为1------------------------- 又∵a>1.的最小值为0---------------- ∴m的取值范围是m≤0-----------------------(14
网址:http://m.1010jiajiao.com/timu3_id_507356[举报]
已知O为坐标原点,点E、F的坐标分别为(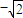 ,0)、(
,0)、(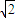 ,0),点A、N满足
,0),点A、N满足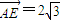 ,
,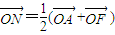 ,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.
,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.
(1)求轨迹C的方程;
(2)若轨迹C上存在两点P和Q关于直线l:y=k(x+1)(k≠0)对称,求k的取值范围;
(3)在(2)的条件下,设直线l与轨迹C交于不同的两点R、S,对点B(1,0)和向量a=(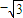 ,3k),求
,3k),求 取最大值时直线l的方程.
取最大值时直线l的方程.
查看习题详情和答案>>
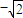 ,0)、(
,0)、(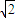 ,0),点A、N满足
,0),点A、N满足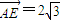 ,
,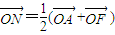 ,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.
,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.(1)求轨迹C的方程;
(2)若轨迹C上存在两点P和Q关于直线l:y=k(x+1)(k≠0)对称,求k的取值范围;
(3)在(2)的条件下,设直线l与轨迹C交于不同的两点R、S,对点B(1,0)和向量a=(
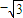 ,3k),求
,3k),求 取最大值时直线l的方程.
取最大值时直线l的方程.查看习题详情和答案>>
(2008•成都三模)已知O为坐标原点,点E、F的坐标分别为(-
,0)、(
,0),点A、N满足
=2
,
=
(
+
),过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.
(1)求轨迹C的方程;
(2)若轨迹C上存在两点P和Q关于直线l:y=k(x+1)(k≠0)对称,求k的取值范围;
(3)在(2)的条件下,设直线l与轨迹C交于不同的两点R、S,对点B(1,0)和向量a=(-
,3k),求
•
-|a|2取最大值时直线l的方程.
查看习题详情和答案>>
| 2 |
| 2 |
| AE |
| 3 |
| ON |
| 1 |
| 2 |
| OA |
| OF |
(1)求轨迹C的方程;
(2)若轨迹C上存在两点P和Q关于直线l:y=k(x+1)(k≠0)对称,求k的取值范围;
(3)在(2)的条件下,设直线l与轨迹C交于不同的两点R、S,对点B(1,0)和向量a=(-
| 3 |
| BR |
| BS |
已知抛物线C:y2=2px(p>0)上任意一点到焦点F的距离比到y轴的距离大1.
(1)求抛物线C的方程;
(2)若过焦点F的直线交抛物线于M、N两点,M在第一象限,且|MF|=2|NF|,求直线MN的方程;
(3)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
,求侧棱长”;也可以是“若正四棱锥的体积为
,求所有侧面面积之和的最小值”.
现有正确命题:过点A(-
,0)的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.
试给出上述命题的“逆向”问题,并解答你所给出的“逆向”问题.
查看习题详情和答案>>
(1)求抛物线C的方程;
(2)若过焦点F的直线交抛物线于M、N两点,M在第一象限,且|MF|=2|NF|,求直线MN的方程;
(3)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积
| 16 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
现有正确命题:过点A(-
| p |
| 2 |
试给出上述命题的“逆向”问题,并解答你所给出的“逆向”问题.
 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为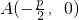 的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.
的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.