题目内容
已知O为坐标原点,点E、F的坐标分别为(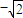 ,0)、(
,0)、(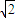 ,0),点A、N满足
,0),点A、N满足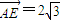 ,
,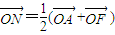 ,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.
,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.(1)求轨迹C的方程;
(2)若轨迹C上存在两点P和Q关于直线l:y=k(x+1)(k≠0)对称,求k的取值范围;
(3)在(2)的条件下,设直线l与轨迹C交于不同的两点R、S,对点B(1,0)和向量a=(
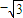 ,3k),求
,3k),求 取最大值时直线l的方程.
取最大值时直线l的方程.
【答案】分析:(Ⅰ)由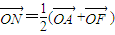 ,可知N为AF中点.则MN垂直平分AF.从而有
,可知N为AF中点.则MN垂直平分AF.从而有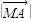 =
=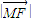 .即可得
.即可得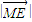 +
+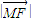 =
=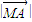 +
+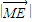 =
=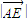 =
=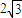 >
>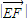 .根据椭圆的定义可知,点M的轨迹C是以正E、F为焦点的椭圆,可求椭圆方程(2)设P(x1,y1),Q(x2,y2),PQ的中点T(x0,y0).由
.根据椭圆的定义可知,点M的轨迹C是以正E、F为焦点的椭圆,可求椭圆方程(2)设P(x1,y1),Q(x2,y2),PQ的中点T(x0,y0).由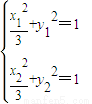 ,两式相减可及y0=k(x0+1)可求
,两式相减可及y0=k(x0+1)可求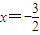 ,
,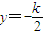 .由中点T(x0,y0)在椭圆内部可求k的范围(3)将y=k(x+1)(k≠0)代入椭圆
.由中点T(x0,y0)在椭圆内部可求k的范围(3)将y=k(x+1)(k≠0)代入椭圆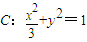 中,整理得(1+3k2)x2+6k2x+3k2-3=0.设R(x3,y3),S(x4,y4).则x3+x4=
中,整理得(1+3k2)x2+6k2x+3k2-3=0.设R(x3,y3),S(x4,y4).则x3+x4=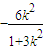 ,x3x4=
,x3x4=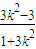 .y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=
.y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=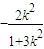 ,代入已知向量的数量积可求k,进而可求直线方程.
,代入已知向量的数量积可求k,进而可求直线方程.
解答:解:(Ⅰ)∵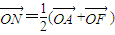 ,
,
∴N为AF中点.
∴MN垂直平分AF.
∴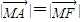 .
.
∴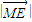 +
+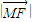 =
=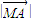 +
+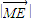 =
=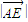 =
=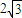 >
>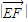 .
.
∴点M的轨迹C是以正E、F为焦点的椭圆.…(2分)
∴长半轴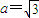 ,半焦距
,半焦距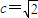 ,
,
∴b2=a2-c2=1.
∴点M的轨迹方程为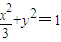 .…(2分)
.…(2分)
(2)设P(x1,y1),Q(x2,y2),PQ的中点T(x,y).
由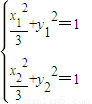 两式相减可得,
两式相减可得,
∴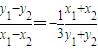
∴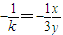
又y=k(x+1)
∴ ,
,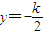 .…(2分)
.…(2分)
∵中点T(x,y)在椭圆内部,
∴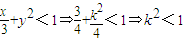
∴k∈(-1,0)∪(0,1).
(3)将y=k(x+1)(k≠0)代入椭圆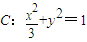 中,整理得(1+3k2)x2+6k2x+3k2-3=0.
中,整理得(1+3k2)x2+6k2x+3k2-3=0.
设R(x3,y3),S(x4,y4).
则x3+x4=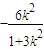 ,x3x4=
,x3x4=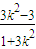 .
.
∴y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=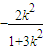 …(2分)
…(2分)
∴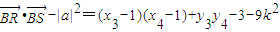
=x3x4-(x3+x4)+1+y3y4-3-9k2
=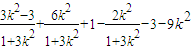 =
=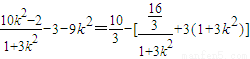
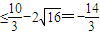 .
.
当且仅当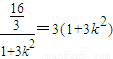 ,即
,即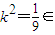 (0,1)时等号成立.
(0,1)时等号成立.
此时,直线l的方程为y=(x+1).…(2分)
点评:本题主要考查了利用向量的基本关系转化线段之间的关系,利用椭圆的定义求解椭圆的方程,及直线与椭圆的相交关系的点差法的应用,直线与曲线相交关系中方程方程的根与系数关系的应用,属于综合性试题
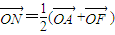 ,可知N为AF中点.则MN垂直平分AF.从而有
,可知N为AF中点.则MN垂直平分AF.从而有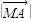 =
=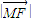 .即可得
.即可得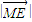 +
+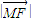 =
=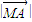 +
+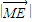 =
=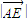 =
=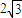 >
>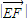 .根据椭圆的定义可知,点M的轨迹C是以正E、F为焦点的椭圆,可求椭圆方程(2)设P(x1,y1),Q(x2,y2),PQ的中点T(x0,y0).由
.根据椭圆的定义可知,点M的轨迹C是以正E、F为焦点的椭圆,可求椭圆方程(2)设P(x1,y1),Q(x2,y2),PQ的中点T(x0,y0).由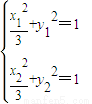 ,两式相减可及y0=k(x0+1)可求
,两式相减可及y0=k(x0+1)可求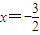 ,
,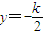 .由中点T(x0,y0)在椭圆内部可求k的范围(3)将y=k(x+1)(k≠0)代入椭圆
.由中点T(x0,y0)在椭圆内部可求k的范围(3)将y=k(x+1)(k≠0)代入椭圆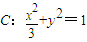 中,整理得(1+3k2)x2+6k2x+3k2-3=0.设R(x3,y3),S(x4,y4).则x3+x4=
中,整理得(1+3k2)x2+6k2x+3k2-3=0.设R(x3,y3),S(x4,y4).则x3+x4=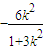 ,x3x4=
,x3x4=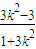 .y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=
.y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=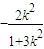 ,代入已知向量的数量积可求k,进而可求直线方程.
,代入已知向量的数量积可求k,进而可求直线方程.解答:解:(Ⅰ)∵
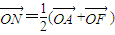 ,
,∴N为AF中点.
∴MN垂直平分AF.
∴
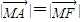 .
.∴
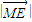 +
+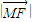 =
=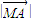 +
+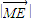 =
=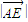 =
=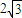 >
>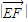 .
.∴点M的轨迹C是以正E、F为焦点的椭圆.…(2分)
∴长半轴
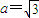 ,半焦距
,半焦距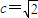 ,
,∴b2=a2-c2=1.
∴点M的轨迹方程为
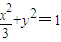 .…(2分)
.…(2分)(2)设P(x1,y1),Q(x2,y2),PQ的中点T(x,y).
由
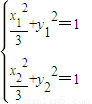 两式相减可得,
两式相减可得,
∴
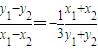
∴
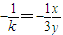
又y=k(x+1)
∴
 ,
,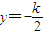 .…(2分)
.…(2分)∵中点T(x,y)在椭圆内部,
∴
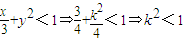
∴k∈(-1,0)∪(0,1).
(3)将y=k(x+1)(k≠0)代入椭圆
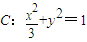 中,整理得(1+3k2)x2+6k2x+3k2-3=0.
中,整理得(1+3k2)x2+6k2x+3k2-3=0.设R(x3,y3),S(x4,y4).
则x3+x4=
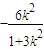 ,x3x4=
,x3x4=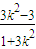 .
.∴y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=
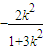 …(2分)
…(2分)∴
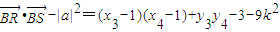
=x3x4-(x3+x4)+1+y3y4-3-9k2
=
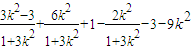 =
=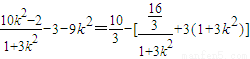
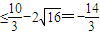 .
.当且仅当
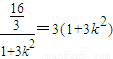 ,即
,即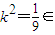 (0,1)时等号成立.
(0,1)时等号成立.此时,直线l的方程为y=(x+1).…(2分)
点评:本题主要考查了利用向量的基本关系转化线段之间的关系,利用椭圆的定义求解椭圆的方程,及直线与椭圆的相交关系的点差法的应用,直线与曲线相交关系中方程方程的根与系数关系的应用,属于综合性试题

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目