摘要:20. 已知:如图.过椭圆作垂直于长轴A1A2 的直线与椭圆c交于P.Q两点.l为左准线. (Ⅰ)求证:直线PA2.A1Q.l共点, (Ⅱ)若过椭圆c左焦点F的直线斜率为k.与椭圆c交于P.Q两点.直线PA2.A1Q.l是否共点.若共点请证明.若不共点请说明理由. 朝阳区2002-2003学年第二学期高三综合练习(一)
网址:http://m.1010jiajiao.com/timu3_id_506616[举报]
 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() 。如图所示,过点F(0,b + 2)作x轴的平行线,与抛物线在第一象限的交点为G。已知抛物线在点G的切线经过椭圆的右焦点F1。
。如图所示,过点F(0,b + 2)作x轴的平行线,与抛物线在第一象限的交点为G。已知抛物线在点G的切线经过椭圆的右焦点F1。
(1)求满足条件的椭圆方程和抛物线方程;
(2)点G、![]() 所在的直线截椭圆的右下区域为D,
所在的直线截椭圆的右下区域为D,
若圆C:![]() 与区域D有公共点,求m的最小值。
与区域D有公共点,求m的最小值。
(本小题满分14分)
如图,已知椭圆
 过点(1,
过点(1, ),离心率为
),离心率为  ,左右焦点分别为
,左右焦点分别为 .点
.点 为直线
为直线 :
: 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 为坐标原点.
为坐标原点.

(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线 、
、 斜率分别为
斜率分别为
 .
.
(ⅰ)证明:
(ⅱ )问直线 上是否存在一点
上是否存在一点 ,使直线
,使直线 的斜率
的斜率 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看习题详情和答案>>
 (ii)试问点
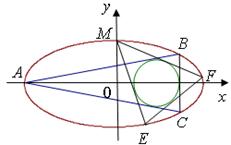
(ii)试问点 如图,已知圆
如图,已知圆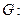
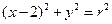 是椭圆
是椭圆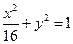 的内接△
的内接△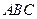 的内切圆, 其中
的内切圆, 其中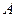 为椭圆的左顶点.
为椭圆的左顶点. 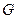 的半径
的半径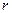 ;
;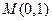 作圆
作圆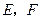 两点,
两点,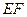 与圆
与圆