摘要:20. 已知:椭圆 (Ⅰ)若点P是椭圆C内部一点.求证: (Ⅱ)若椭圆上存在不同的两点关于直线对称.试求.满足的关系式. 朝 阳 区 高 三 统 一 练 习(二)
网址:http://m.1010jiajiao.com/timu3_id_506596[举报]
(本小题满分14分)
已知F1,F2分别是椭圆+=1的左、右焦点,曲线C是以坐标原点为顶点,以F2为焦点的抛物线,自点F1引直线交曲线C于P、Q两个不同的交点,点P关于x轴的对称点记为M.设=λ.
(Ⅰ)求曲线C的方程;
(Ⅱ)证明:=-λ;
(Ⅲ)若λ∈[2,3],求|PQ|的取值范围.
查看习题详情和答案>>
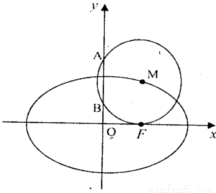
(本小题满分14分)已知点F椭圆E: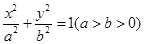 的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且
的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且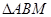 是边长为2的正三角形;又椭圆E上的P、Q两点关于直线
是边长为2的正三角形;又椭圆E上的P、Q两点关于直线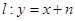 对称.
对称.
(1)求椭圆E的方程;(2)当直线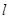 过点(
过点(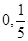 )时,求直线PQ的方程;
)时,求直线PQ的方程;
(3)若点C是直线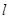 上一点,且
上一点,且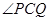 =
=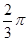 ,求
,求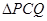 面积的最大值.
面积的最大值.
查看习题详情和答案>>
(本小题满分14分)已知点F椭圆E: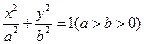 的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且
的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且 是边长为2的正三角形;又椭圆E上的P、Q两点关于直线
是边长为2的正三角形;又椭圆E上的P、Q两点关于直线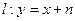 对称.
对称.
(1)求椭圆E的方程;(2)当直线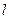 过点(
过点(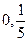 )时,求直线PQ的方程;
)时,求直线PQ的方程;
(3)若点C是直线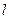 上一点,且
上一点,且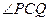 =
=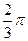 ,求
,求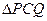 面积的最大值.
面积的最大值.
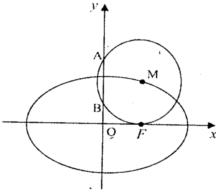
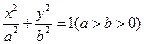 的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且
的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且 是边长为2的正三角形;又椭圆E上的P、Q两点关于直线
是边长为2的正三角形;又椭圆E上的P、Q两点关于直线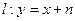 对称.
对称.(1)求椭圆E的方程;(2)当直线
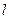 过点(
过点(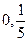 )时,求直线PQ的方程;
)时,求直线PQ的方程;(3)若点C是直线
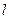 上一点,且
上一点,且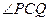 =
=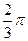 ,求
,求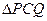 面积的最大值.
面积的最大值.
 =
=  ;
; +
+ =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之. 经过椭圆S:
经过椭圆S: 的一个焦点和一个顶点.
的一个焦点和一个顶点. 轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.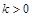 ,求证:
,求证: .
.