摘要:6.在区间[100,200]上的正整数中,被3除余2的数的个数是 A.32 B.33 C.34 D.35 txjy
网址:http://m.1010jiajiao.com/timu3_id_505690[举报]
 某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.(1)完成下面的2×2列联表;
| 不喜欢运动 | 喜欢运动 | 合计 | |
| 女生 | 50 | ||
| 男生 | |||
| 合计 | 100 | 200 |
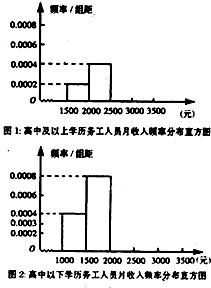 (2011•临沂二模)某地外出务工人员有1000人,其中高中及以上学历的有800人,高中以下学历有200人,现用分层抽样的方法从该地外出务工人员中抽查100人,调查他们的月收入情况,从高中及以上学历人群中抽查结果和从高中以下学历人群中抽查结果分别如表1和表2.
(2011•临沂二模)某地外出务工人员有1000人,其中高中及以上学历的有800人,高中以下学历有200人,现用分层抽样的方法从该地外出务工人员中抽查100人,调查他们的月收入情况,从高中及以上学历人群中抽查结果和从高中以下学历人群中抽查结果分别如表1和表2.表1:
| 月收入(单位元) | [1500,2000) | [2000,2500) | [2500,3000) | [3000,3500) |
| 人数 | 8 | 16 | x | 24 |
| 月收入(单位元) | [1000,1500) | [1500,2000) | [2000,2500) | [2500,3000) | [3000,3500) |
| 人数 | 4 | 8 | 3 | y | 2 |
(II)(1)估计高中及以上学历外出务工人员月收入的平均值与高中以下外出务工人员月收入的平均值哪个更高;
(2)在抽查的100人中从高中以下学历月收入在2000~3000元之间的人员中,抽查两人了解其工作环境,求抽查的两人中至少有
1人月收入不少于2500元的概率.
某种家用电器的销售利润与该电器的无故障使用时间有关.每台这种家用电器,若无故障使用时间不超过一年,则销售利润为0元;若无故障使用时间超过一年不超过三年,则销售利润为100元;若无故障使用时间超过三年,则销售利润为200元.己知每台这种家用电器无故障使用时间不超过一年的概率为
,无故障使用时间超过一年不超过三年的概率为
.记ξ表示销售两台这种家用电器的销售利润总和.
(Ⅰ) 求ξ的分布列及数学期望;
(Ⅱ)设“函数f(x)=x2-
ξx-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率.
查看习题详情和答案>>
| 1 |
| 5 |
| 2 |
| 5 |
(Ⅰ) 求ξ的分布列及数学期望;
(Ⅱ)设“函数f(x)=x2-
| 1 |
| 100 |
 某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:(1)根据上面的频率分布表,求①,②,③,④处的数值;
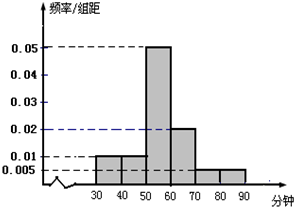
(2)根据上面的频率分布表,在所给的坐标系中画出在区间[80,150]上的频率分布直方图;
(3)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从总体中任意抽取3个个体,成绩落在[100,120]中的个体数为ξ,求ξ的分布列和数学期望.
| 分组 | 频数 | 频率 |
| [80,90) | ① | ② |
| [90,100) | 0.050 | |
| [100,110) | 0.200 | |
| [110,120) | 36 | 0.300 |
| [120,130) | 0.275 | |
| [130,140) | 12 | ③ |
| [140,150) | 0.050 | |
| 合计 | ④ |
(本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的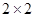 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和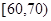 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.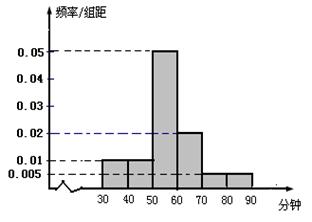 查看习题详情和答案>>
查看习题详情和答案>>