题目内容
 某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.(1)完成下面的2×2列联表;
| 不喜欢运动 | 喜欢运动 | 合计 | |
| 女生 | 50 | ||
| 男生 | |||
| 合计 | 100 | 200 |
分析:(1)根据分层抽样的定义,知抽取男生130人,女生70人,将数据填入相应位置.
(2)利用古典概型概率公式求解即可.
(2)利用古典概型概率公式求解即可.
解答:解:(1)根据分层抽样的定义,知抽取男生130人,女生70人,…(1分)
…(3分)
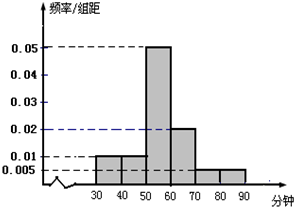
(2)由直方图知在[60,70)内的人数为4人,设为a,b,c,d.
在[40,50)的人数为2人,设为A,B.…(5分)
从这6人中任选2人有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd
共15种情况 …(7分)
若x,y∈[60,70)时,有ab,ac,ad,bc,bd,cd共六种情况. …(9分)
若x,y∈[40,50)时,有AB一种情况. …(10分)
事件A:“她们在同一区间段”所包含的基本事件个数有6+1=7种,…(11分)
故 P(A)=
答:两名女生的运动时间在同一区间段的概率为
.…(12分)
| 不喜欢运动 | 喜欢运动 | 合计 | |
| 女生 | 50 | 20 | 70 |
| 男生 | 50 | 80 | 130 |
| 合计 | 100 | 100 | 200 |
(2)由直方图知在[60,70)内的人数为4人,设为a,b,c,d.
在[40,50)的人数为2人,设为A,B.…(5分)
从这6人中任选2人有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd
共15种情况 …(7分)
若x,y∈[60,70)时,有ab,ac,ad,bc,bd,cd共六种情况. …(9分)
若x,y∈[40,50)时,有AB一种情况. …(10分)
事件A:“她们在同一区间段”所包含的基本事件个数有6+1=7种,…(11分)
故 P(A)=
| 7 |
| 15 |
答:两名女生的运动时间在同一区间段的概率为
| 7 |
| 15 |
点评:考查统计抽样中数据的处理以及古典概率模型,属于基础技能题型.

练习册系列答案
相关题目
(本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的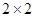 列联表;
列联表;
|
|
不喜欢运动 |
喜欢运动 |
合计 |
|
女生 |
50 |
|
|
|
男生 |
|
|
|
|
合计 |
|
100 |
200 |
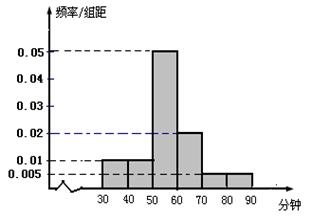
(2)在喜欢运动的女生中调查她们的运动时间, 发现她们的运动时间介于30分钟到90分钟之间,如图是测量结果的频率分布直方图,若从区间段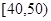 和
和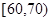 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的2×2列联表;
(2)在喜欢运动的女生中调查她们的运动时间,发现她们的运动时间介于30分钟到90分钟之间,右图是测量结果的频率分布直方图,若从区间段[40,50)和[60,70)的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
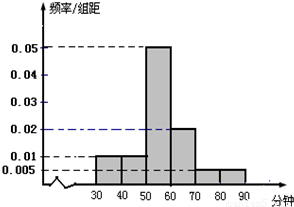
(1)完成下面的2×2列联表;
| 不喜欢运动 | 喜欢运动 | 合计 | |
| 女生 | 50 | ||
| 男生 | |||
| 合计 | 100 | 200 |
