摘要：21． 已知数列{an}的首项是以p为公比的等比数列. {an}的前n项和为 (1)试问:S1.S2.S3--.Sn.--能否构成等差数列或等比数列.给出证明, (2)设
网址：http://m.1010jiajiao.com/timu3_id_505372[举报]
（本题满分12分） 已知函数
.
(Ⅰ) 求f 1(x)；
(Ⅱ) 若数列{an}的首项为a1=1，
(nÎN+)，求{an}的通项公式an；
(Ⅲ) 设bn=an+12+an+22+¼+a2n+12，是否存在最小的正整数k，使对于任意nÎN+有bn<
成立. 若存在，求出k的值；若不存在，说明理由.
. （本题满分12分）已知函数
.(Ⅰ) 求f –1(x)；(Ⅱ) 若数列{an}的首项为a1=1，
(n??N+)，求{an}的通项公式an；(Ⅲ) 设bn=an+12+an+22+??+a2n+12，是否存在最小的正整数k，使对于任意n??N+有bn<
成立. 若存在，求出k的值；若不存在，说明理由.
（本题满分12分）已知函数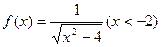
.(Ⅰ) 求f –1(x)；(Ⅱ) 若数列{an}的首项为a1=1，
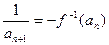(nÎN+)，求{an}的通项公式an；(Ⅲ) 设bn=an+12+an+22+¼+a2n+12，是否存在最小的正整数k，使对于任意nÎN+有bn<
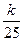成立.若存在，求出k的值；若不存在，说明理由.
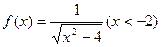.(Ⅰ) 求f –1(x)；(Ⅱ) 若数列{an}的首项为a1=1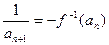，(nÎN+)，求{an}的通项公式an；(Ⅲ) 设bn=an+12+an+22+¼+a2n+12，是否存在最小的正整数k，使对于任意nÎN+有bn<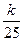成立.若存在，求出k的值；若不存在，说明理由.
、
、
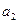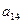分别是一个等比数列的第二项、第三项、第四项．
＝
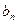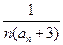（n∈N*），
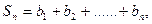求
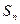
<0.001成立的最小的n值.