摘要:已知向量m=(1.1).向量n与向量m的夹角为,且m·n=-1. (1)求向量n, (2)设向量a=(1.0).向量b=(cosx,2cos2()),其中0<x<.若n·a=0,试求|n+b|的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_503410[举报]
(本小题满分12分)
已知向量m=(sin,1),n=(cos,cos2),f(x)=m·n.
(1)若f(x)=1,求cos(-x)的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.
查看习题详情和答案>>
(本小题满分12分)
已知向量m=(sin,1),n=(cos,cos2),f(x)=m·n.
(1)若f(x)=1,求cos(-x)的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.
已知向量m=(sin,1),n=(cos,cos2),f(x)=m·n.
(1)若f(x)=1,求cos(-x)的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.
(本小题满分12分)已知向量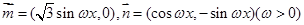 ,在函数
,在函数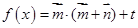 的图像上,对称中心到对称轴的最小距离为
的图像上,对称中心到对称轴的最小距离为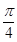 ,且当
,且当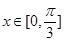 时
时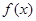 的最小值为
的最小值为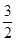 。
。
(1)求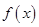 的解析式;
的解析式;
(2)求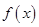 的单调递增区间;
的单调递增区间;
(3)若对任意x1,x2∈[0,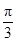 ]都有
]都有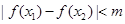 ,求实数m的取值范围。
,求实数m的取值范围。
查看习题详情和答案>>
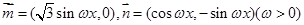 ,在函数
,在函数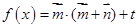 的图像上,对称中心到对称轴的最小距离为
的图像上,对称中心到对称轴的最小距离为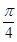 ,且当
,且当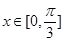 时
时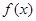 的最小值为
的最小值为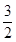 。
。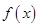 的解析式;
的解析式;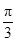 ]都有
]都有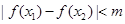 ,求实数
,求实数 m的取值范围。
m的取值范围。