题目内容
若函数f（x）=xlnx在x0处的函数值与导数值之和等于1，则x0的值等于（ ）
分析：先对函数进行求导，然后根据在x0处的函数值与导数值之和等于1，建立等式关系，解之即可求得答案．
解答：解：∵f（x）=xln x，（x＞0）
∴f（x0）=x0lnx0，f′（x）=lnx+1，
∴f′（x0）=lnx0+1，
∵函数f（x）=xln x在x0处的函数值与导数值之和等于1，
∴f（x0）+f′（x0）=x0lnx0+lnx0+1=1，
解得x0=1，
∴x0的值等于1．
故选A．
∴f（x0）=x0lnx0，f′（x）=lnx+1，
∴f′（x0）=lnx0+1，
∵函数f（x）=xln x在x0处的函数值与导数值之和等于1，
∴f（x0）+f′（x0）=x0lnx0+lnx0+1=1，
解得x0=1，
∴x0的值等于1．
故选A．
点评：本题主要考查了导数的运算，以及函数求值和对数方程的求解，同时考查了运算求解的能力，注意函数的定义域，属于基础题．
练习册系列答案
综合自测系列答案
相关题目
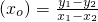，求证：xo＞xl．
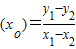，求证：xo＞xl．