摘要:18.定义在R上的函数f(x)对任意实数a.b都有f(a + b)+ f(a - b)= 2f(a)·f(b)成立.且f(0)≠0. (1)求f(0); (2)证明f(x)的奇偶性, (3)若存在常数c>0使f()=0.试问f(x)是否为周期函数.若是.指出它的一个周期.若不是请说明理由..
网址:http://m.1010jiajiao.com/timu3_id_500869[举报]
定义在R上的函数f(x)对任意实数a、b都有f(a+b)+f(a-b)=2f(a)·f(b)成立,且f(0)≠0.
(1)求f(0);
(2)证明f(x)的奇偶性;
(3)若存在常数c>0使f( )=0,试问f(x)是否为周期函数.若是,指出它的一个周期,若不是请说明理由.
)=0,试问f(x)是否为周期函数.若是,指出它的一个周期,若不是请说明理由.
已知定义在R上的函数f(x)对任意实数 ,
, 满足关系f(
满足关系f( +
+ )=f(
)=f( )+f(
)+f( )+2.
)+2.
(1)证明:f(x)的图象关于点(0,-2)对称. (2)若x>0,则有f(x)>-2,求证:f(x)在R上为增函数.
(3)若数列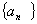 满足
满足 =-
=- ,且对任意n∈N有
,且对任意n∈N有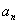 =f(n),试求数列
=f(n),试求数列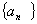 的前n项和
的前n项和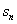 .
查看习题详情和答案>>
.
查看习题详情和答案>>
(1)证明:f(x)的图象关于点(0,-2)对称. (2)若x>0,则有f(x)>-2,求证:f(x)在R上为增函数.
(3)若数列
已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=- .
.
(1)求证:f(x)为奇函数; (2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
 .
. .
.