题目内容
已知定义在R上的函数f(x)对任意实数(1)证明:f(x)的图象关于点(0,-2)对称. (2)若x>0,则有f(x)>-2,求证:f(x)在R上为增函数.
(3)若数列
解析:(1)证明:在已知恒等式中令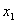 =
=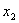 =0得f(0)=-2① 又已知恒等式中令
=0得f(0)=-2① 又已知恒等式中令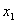 =x,
=x, 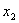 =-x得f(0)=f(x)+f(-x)+2
=-x得f(0)=f(x)+f(-x)+2
∴f(x)+f(-x)=-4 ② 设M(x,f(x))为y=f(x)的图象上任意一点则由②得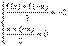 ③
③
∴由③知点M(x,f(x))与N(-x,f(-x))所成线段MN的中点坐标为(0,-2), ∴点M与点N关于定点(0,-2)对称. ④
注意到点M在y=f(x)图象上的任意性,又点N亦在y=f(x)的图象上,故由④知y=f(x)的图象关于点(0,-2)对称.
(2)证明:设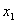 ,
,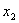 为任意实数,且
为任意实数,且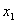 <
<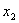 ,则
,则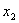 -
-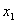 >0 ∴由已知得f(
>0 ∴由已知得f(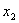 -
-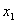 )>-2 ⑤
)>-2 ⑤
注意到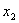 =(
=(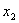 -
-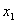 )+
)+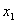 由本题大前提中的恒等式得 f(
由本题大前提中的恒等式得 f(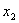 )=f[(
)=f[(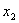 -
-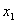 )+
)+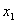 ] =f(
] =f(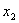 -
-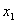 )+ f(
)+ f(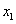 )+2
)+2
∴f(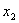 )-f(
)-f(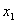 )=f (
)=f (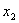 -
-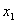 )+2 ⑥ 又由⑤知f (
)+2 ⑥ 又由⑤知f (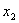 -
-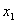 )+2>0, ∴由⑥得f(
)+2>0, ∴由⑥得f(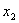 )-f(
)-f(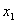 )>0,即f(
)>0,即f(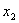 )>f(
)>f(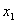 ).
).
于是由函数的单调性定义知,f(x)在R上为增函数.
(3)解: ∵an=f(n), ∴a1=f(1)=-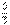 , an+1=f(n+1)
, an+1=f(n+1)
又由已知恒等式中令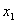 =n,
=n, 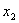 =1得 f(n+1)=f(n)+f(1)+2 ∴an+1= an+
=1得 f(n+1)=f(n)+f(1)+2 ∴an+1= an+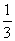 ∴an+1-an=
∴an+1-an=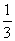 (n∈N)
(n∈N)
由此可知,数列{ an }是首项为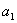 =-
=-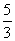 ,公差为
,公差为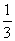 的等差数列. ∴
的等差数列. ∴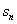 =-
=-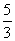 n+
n+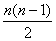 ×
×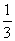 即
即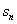 =
=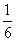 (n2-11n).
(n2-11n).
∴f(x)+f(-x)=-4 ② 设M(x,f(x))为y=f(x)的图象上任意一点则由②得
∴由③知点M(x,f(x))与N(-x,f(-x))所成线段MN的中点坐标为(0,-2), ∴点M与点N关于定点(0,-2)对称. ④
注意到点M在y=f(x)图象上的任意性,又点N亦在y=f(x)的图象上,故由④知y=f(x)的图象关于点(0,-2)对称.
(2)证明:设
注意到
∴f(
于是由函数的单调性定义知,f(x)在R上为增函数.
(3)解: ∵an=f(n), ∴a1=f(1)=-
又由已知恒等式中令
由此可知,数列{ an }是首项为

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |