摘要:从题设条件出发.运用定义.定理.公式.性质.法则等知识.通过变形.推理.计算等.得到正确的结论. [例1] 的展开式中的系数为 . 解: 得展开式中的系数为=179. [类比1] 已知函数在区间上为增函数.则实数的取值范围 是 . [类比2] 函数.在中的最大值比最小值大.则的值 为 . [类比3] 在等差数列中.若.则等式 ()成立.类比上述性质.相应地.在等比数列中.若.则有等 式 成立. [类比4] 已知是直线.是平面.给出下列命题: ①若...则.或, ②若...则, ③若不垂直.则不可能垂直于内无数条直线, ④若..且..则且. 其中正确的命题的序号是 .(注:把你认为正确的命题的序号都填上)
网址:http://m.1010jiajiao.com/timu3_id_500317[举报]
 如图,己知|
如图,己知|| OA |
| OB |
| OP |
| OA |
| OB |
| A、①②④ | B、①③④ |
| C、①③⑤ | D、②⑤ |
(2013•长春一模)对于非空实数集A,记A*={y|?x∈A,y≥x}.设非空实数集合M、P满足:M⊆P,且若x>1,则x∉P.现给出以下命题:
①对于任意给定符合题设条件的集合M、P,必有P*⊆M*;
②对于任意给定符合题设条件的集合M、P,必有M*∩P≠∅;
③对于任意给定符合题设条件的集合M、P,必有M∩P*=∅;
④对于任意给定符合题设条件的集合M、P,必存在常数a,使得对任意的b∈M*,恒有a+b∈P*,
其中正确的命题是( )
①对于任意给定符合题设条件的集合M、P,必有P*⊆M*;
②对于任意给定符合题设条件的集合M、P,必有M*∩P≠∅;
③对于任意给定符合题设条件的集合M、P,必有M∩P*=∅;
④对于任意给定符合题设条件的集合M、P,必存在常数a,使得对任意的b∈M*,恒有a+b∈P*,
其中正确的命题是( )
查看习题详情和答案>>
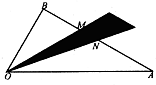
 ,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,
,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点, ,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,①x≥0,y≥0;②x-y≥0;③x-y≤0;④5x-3y≥0;⑤3x-5y≥0.满足题设条件的为( )
,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,①x≥0,y≥0;②x-y≥0;③x-y≤0;④5x-3y≥0;⑤3x-5y≥0.满足题设条件的为( )
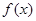 的定义域内任意一个
的定义域内任意一个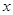 的值,均有
的值,均有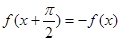 ,且
,且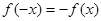 ,对于下列五个函数:①
,对于下列五个函数:①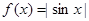 ;②
;②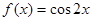 ; ③
; ③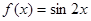 ;④
;④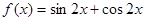 ,其中适合题设条件的函数的序号是 .
,其中适合题设条件的函数的序号是 . 的定义域内任意一个
的定义域内任意一个 的值,均有
的值,均有 ,且
,且 ,对于下列五个函数:①
,对于下列五个函数:① ;②
;② ; ③
; ③ ;④
;④ ,其中适合题设条件的函数的序号是 .
,其中适合题设条件的函数的序号是 .