Question

如图，己知|

OA

|=5，|

OB

|=3，∠AOB为锐角，OM平分∠AOB，点N为线段AB的中点，

OP

=x

OA

+y

OB

，若点P在阴影部分（含边界）内，则在下列给出的关于x、y的式子中，①x≥0，y≥0；②x-y≥0；③x-y≤0；④5x-3y≥0；⑤3x-5y≥0．满足题设条件的为（　　）

• A、①②④
• B、①③④
• C、①③⑤
• D、②⑤

Answer 1

分析：利用向量共线定理，及三角形法则，将向量

OP

用

OA

，

OB

表示出来，

OA

，

OB

的系数对应等于x，y．由此即可解题

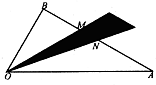
解答：解：设线段OP与AB的交点为C，
则由向量共线定理知：存在实数λ，

OP

=λ

OC

，其中λ＞0，
∴

OP

=λ

OC

=λ(

OA

+

AC

)
=λ

OA

+λ

AC

，
∵

AC

，

AB

共线，
∴存在实数μ，使得

AC

=μ

AB

，
∵N为AB的中点，
∴μ＞

1

2

'
又∵|

OA

|=5，|

OB

|=3，OM平分∠AOB，
∴由正弦定理知，AM=

5

3

BM
∴AC≤AM=

5

8

AB，
故

1

2

＜μ≤

5

8

，
∴

OP

=λ

OA

+λμ

AB

=λ

OA

+λμ(

OB

-

OA

)
=λ(1-μ)

OA

+λμ

OB

∴x=λ（1-μ），y=λμ，
∴x≥0，y≥0；
∴x-y=λ（1-2μ）≤0；
∴5x-3y=λ（5-8μ）≥0．
故选：B．

点评：本题主要考察了平面向量的共线定理以及向量的三角形法则，并涉及到了正弦定理，难度较大，属于难题．