摘要:12.设G.M分别为不等边△ABC的重心与外心.A.GM//AB. (1)求点C的轨迹方程, (2)设点C的轨迹为曲线E.是否存在直线.使过点(0.1)并与曲线E交于P.Q两点.且满足?若存在.求出直线的方程.若不存在.说明理由. 注:三角形的重心的概念和性质如下:设△ABC的重心.且有. 解:(I)点C的轨迹方程为 x2+ (II)假设存在直线满足条件.设直线方程为y=kx+1, 由消去x.得(3+k2)x2+2kx-2=0 ∵直线与曲线E并于P.Q两点.∴△=4k2+8(2+k2)>0 设P(x1,y1).Q(x2,y2),则 ∵ ∴x1x2+y1y2=-2,即x1x2+(kx1+1)(kx2+1)=-2. (1+k2)x1x2+k(x1+x2)+3=0, (1+k2) 解得k2=7, ∴k=± 故存在直线:y=±+1,使得
网址:http://m.1010jiajiao.com/timu3_id_500090[举报]
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),GM∥AB.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
•
=-2?若存在,求出直线l的方程,若不存在,说明理由.
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
=
=
=
.
查看习题详情和答案>>
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
| OP |
| OQ |
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),GM∥AB.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足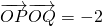 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.
注:三角形的重心的概念和性质如下:设△ABC的重心,且有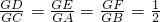 .
.
查看习题详情和答案>>
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),GM∥AB.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
•
=-2?若存在,求出直线l的方程,若不存在,说明理由.
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
=
=
=
.
查看习题详情和答案>>
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
| OP |
| OQ |
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |