题目内容
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),且(1)求点C的轨迹E的方程;
(2)是否存在直线z,使Z过点(0,1)并与曲线E交于P、Q两点,且满足OP⊥OQ?若存在,求出直线l的方程;若不存在,说明理由.
答案:(1)设C(x,y),则G(![]() ),其中x·y≠0.
),其中x·y≠0.
设外心M(0,m),而GM∥AB,
即(![]() )∥(2,0),则m=
)∥(2,0),则m=![]() .
.
由|MA|=|MC|,得
![]() ,
,
整理得轨迹E的方程是3x2+y2=3(xy≠0).
(2)假设存在直线l满足题设条件,由题设知l的方程
为y=kx+1,代入3x2+y2=3,
化简得(k2+3)x2+2kx-2=0,
则△=4k2+8(k2+3)>0.
设P(x1,kx1+1),Q(x2,kx2+1)
∴x1+x2=![]() ①
①
x1x2=![]() ②
②
由OP⊥OQ,即![]() =0,得
=0,得
(kx1+1)(kx2+1)+x1x2=0
即(k2+1)x1x2+k(x1+x2)+1=0.
结合①②得3k2=1,则k=±![]() ,
,
故存在直线l:y=±![]() x+1,使得OP⊥OQ.
x+1,使得OP⊥OQ.

练习册系列答案
相关题目
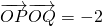 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.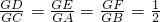 .
.